5141. НОК сумма
По заданному
значению n вычислите
сумму НОК(1, n)
+ НОК(2, n) + ..
+ НОК(n, n), где НОК(i, n) обозначает
Наименьшее Общее Кратное чисел i и n.
Вход. Первая строка
содержит количество тестов t (1
≤ t ≤ 300000). Каждая из
следующих t строк содержит одно целое
число n (1 ≤ n ≤ 106).
Выход. Выведите t строк, каждая из которых содержит
требуемую сумму.
|
Пример
входа |
Пример
выхода |
|
3 1 2 5 |
1 4 55 |
РЕШЕНИЕ
теория чисел
Анализ алгоритма
Пусть S =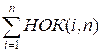 
= 
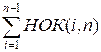+ НОК(n, n)
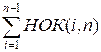= + n, откуда
S – n = НОК(1, n) + НОК(2, n) + . . . +
НОК(n – 1, n)
Переставим
слагаемые в правой части в обратном порядке и запишем равенство в виде
S – n = НОК(n – 1, n) + . . . +
НОК(2, n) + НОК(1, n)
Сложим два равенства:
2(S – n) = (НОК(1, n) + НОК(n – 1, n)) + . . . + (НОК(n – 1,
n)
+ НОК(1, n))
Рассмотрим
выражение в скобках:
НОК(i, n) + НОК(n
– i, n) =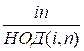 
+ 
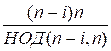
Заметим, что
знаменатели последних двух слагаемых равны: НОД(i, n) = НОД(n – i,
n), следовательно
+ = 
=
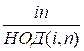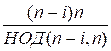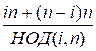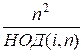
Откуда
2(S – n) =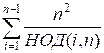 
= 
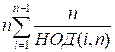
НОД(i, n) = d
может принимать только значения делителей числа n, при этом количество i
для которых имеет место указанное равенство, равно φ (n / d). Следовательно
2(S – n) = =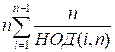 
= 
= 
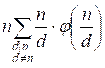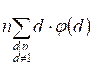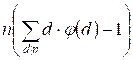
Второе равенство справедливо так как если d делитель n, то n / d также делитель n. При этом если d
≠ n, то n / d ≠ 1.
Последнее равенство справедливо, так как в сумму включили слагаемое 1 * φ
(1) = 1. Осталось выделить из уравнения значение S:
2(S – n) = 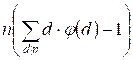, 2S – 2n = 
,
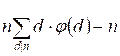S =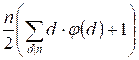 
Реализация алгоритма
#define
MAX 1000001
long long res[MAX], phi[MAX];
Функция FillEuler заполняет массив phi[i] = φ(i).
void
FillEuler(void)
{
int i, j;
phi[1] = 1;
for(i = 2; i < MAX; i++) phi[i] = i;
for(i = 2; i < MAX; i+=2) phi[i] /=
2;
for(i = 3; i < MAX; i+=2)
if (phi[i] == i)
for(j = i; j < MAX; j += i) phi[j] -=
phi[j]/i;
}
Основная часть программы. Заполняем массив phi значениями функции Эйлера.
FillEuler();
После выполнения следующего цикла res[n] =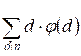 
.
Для
каждого значения i, являющегося делителем j, к res[j] прибавляется i * φ(i).
for(i
= 1; i < MAX; i++)
for(j
= i; j < MAX; j += i)
res[j] += (i * phi[i]);
Читаем входные данные. Последовательно обрабатываем тесты.
Вычисляем и выводим ответ.
scanf("%d",&tests);
while(tests--)
{
scanf("%d",&n);
ans = (res[n] + 1) * n / 2;
printf("%lld\n",ans);
}