5141. LCM sum
Given n, calculate the sum LCM(1, n) + LCM(2, n) + … + LCM(n, n), where LCM(i, n) denotes the Least Common Multiple
of the integers i and n.
Input. First line
contains the number of test cases t (1 ≤ t ≤ 300000). Each of
the next t lines contains an
integer n (1 ≤ n ≤ 106).
Output. Print t lines, one for each test case,
containing the required sum.
|
Sample
input |
Sample
output |
|
3 1 2 5 |
1 4 55 |
SOLUTION
number theory
Algorithm analysis
Let S = 
= 
+ LCM(n, n)
= 
+ n, wherefrom
S – n = LCM(1, n) + LCM(2, n) + . . . + LCM(n – 1, n)
Rearrange the
terms in the right side
in reverse order and write the equality in the form
S – n = LCM(n – 1, n) + . . . + LCM(2, n) + LCM(1, n)
Let's add two
equalities:
2(S – n) = (LCM(1, n) + LCM(n – 1, n)) + . . . + (LCM(n – 1, n)
+ LCM(1, n))
Consider the
expression in parentheses:
LCM(i, n) + LCM(n – i, n)
= 
+ 
Note that the
denominators of the last two terms are equal: GCD(i, n) = GCD(n – i,
n), hence
+ = 
=
So
2(S – n) = 
= 
GCD(i, n) = d
can take only the values of divisors of the number n, while the number of i for which the specified equality holds is φ (n / d).
Hence
2(S – n) = = 
= 
= 
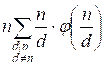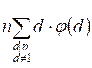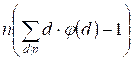
The second equality is true because if d is a divisor of n, then n / d is also a divisor of n. Moreover, if d ≠ n, then n / d ≠ 1. The last equality is valid, since the summand 1 *
φ (1) = 1 is included in the sum. It remains to extract the value S from the equation:
2(S – n) = ,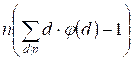
2S – 2n =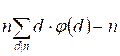 
,
S =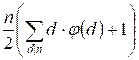 
Algorithm realization
Declare
the arrays.
#define MAX 1000001
long long
res[MAX], phi[MAX];
Function FillEuler fills the array phi[i] = φ(i).
void FillEuler(void)
{
int i, j;
phi[1] = 1;
for(i = 2; i
< MAX; i++) phi[i] = i;
for(i = 2; i
< MAX; i+=2) phi[i] /= 2;
for(i = 3; i
< MAX; i+=2)
if (phi[i]
== i)
for(j =
i; j < MAX; j += i) phi[j] -= phi[j]/i;
}
The main part of the program. Fill the array phi with the values of the Euler function.
FillEuler();
After the execution of the next part of the program res[n] =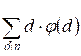 
. For each value of i that is a divisor of j,
i * φ(i) is added to res[j].
for(i = 1; i < MAX; i++)
for(j = i; j < MAX; j += i)
res[j] += (i * phi[i]);
Read the input data. Process tests sequentially. Compute and print the
answer.
scanf("%d",&tests);
while(tests--)
{
scanf("%d",&n);
ans = (res[n] + 1) * n / 2;
printf("%lld\n",ans);
}