5156. Отрезки
Директор Института Геометрии
Отрезков (ИГО) принял Ааза в своём кабинете. Судя по обстановке, институт не
бедствовал. Проблема на этот раз была в другом.
Мы не стоим без работы.
Каждый раз, после начала сезона в чемпионатах по программированию, мы решаем
множество задач на пересечение двух отрезков по заказу организаторов
соревнований. Но это всё-таки рутина, и сотрудники начинают терять интерес.
Кое-где даже вместо работы занимаются самодеятельностью – устраивают концерты для баяна при свечах.
Можете ли сформулировать для нас задачу, отличную от этой, но не очень далеко
от неё ушедшую по формулировке.
Ну например... Дано n отрезков на прямой. Для каждого
отрезка требуется вычислить количество отрезков, которые имеют с ним хотя бы
одну общую точку.
Сотрудники ИГО с энтузиазмом
взялись за задачу. Более того – они поручили Вам написать программу для её
решения.
Вход. Содержит один или несколько
тестов. В первой строке каждого теста записано количество отрезков n (1 ≤ n ≤ 100000). Следующие n
строк описывают отрезки: i-я строка
содержит пару целых чисел Li
и Ri – координаты начала и
конца i-го отрезка (-109
≤ Li ≤ Ri ≤ 109).
Общая сумма значений n во входных
данных не превосходит 100000. Входные данные завершаются нулём. Количество
тестов не превосходит 10000.
Выход. Для каждого теста в одной строке выведите n чисел как показано в примере: i-ое число – количество отрезков, с которыми i-ый отрезок имеет хотя бы одну общую
точку, не считая его самого. Следуйте формату вывода максимально точно.
|
Пример входа |
Пример выхода |
|
3 1 2 2 3 3 4 4 1 6 2 3 4 5 7 8 0 |
Case 1: 1 2 1 Case 2: 2 1 1 0 |
РЕШЕНИЕ
бинарный поиск
Анализ алгоритма
Отсортируем
начала отрезков в одном массиве, а концы отрезков – в другом. Для каждого
отрезка [Li, Ri] при помощи бинарного поиска
вычислим количество отрезков, которые были открыты до Ri включительно, а также количество отрезков, которые
были закрыты до Li не
включительно. Разница между этими количествами, уменьшенная на единицу (сам i-ый отрезок мы не считаем), и есть
число отрезков, имеющих с i-ым хотя
бы одну общую точку.
Пример
Множество отрезков приведенные в
примерах, имеют вид:

Рассмотрим следующее множество
отрезков:

Отсортируем
левые и правые концы отрезков:
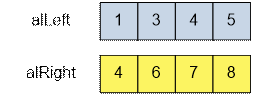
Рассмотрим
первый отрезок [1; 4]:
1.
Найдем количество отрезков, открытых до x = 4
включительно. Для этого совершим бинарный поиск 4 в массиве alLeft по верхней
границе (upper_bound).
2.
Найдем количество отрезков, закрытых до x = 1 не
включая 1. Для этого совершим бинарный поиск 1 в массиве alRight по нижней
границе (lower_bound).
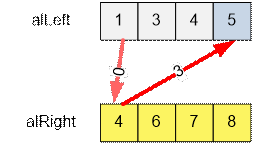
Количество
открытых до завершения [1; 4] имеется 3 отрезка (с абсциссами x = 1, x = 3, x = 4),
количество закрытых до начала [1; 4] имеется 0 отрезков. Отрезок [1; 4]
пересекается с (3 – 0) – 1 = 2 отрезками.
Реализация
алгоритма
Данные об i-ом отрезке храним в паре (left[i], right[i]). Левые
концы отрезков сортируем в массиве alLeft, правые – в alRight.
#define MAX 100010
int
left[MAX], right[MAX];
int
alLeft[MAX], alRight[MAX];
Читаем входные данные.
while
(scanf("%d",&n),n)
{
for(i = 0; i
< n; i++)
{
scanf("%d
%d",&left[i],&right[i]);
alLeft[i] = left[i]; alRight[i] = right[i];
}
Сортируем левые и правые концы
отрезков в отдельных массивах.
sort(alLeft, alLeft + n);
sort(alRight, alRight + n);
Выводим номер теста.
printf("Case
%d:",test++);
Для каждого отрезка (left[i], right[i]) вычисляем разницу между количеством открытых отрезков до Ri включительно и количеством закрытых отрезков до Li не включительно. Вычитая единицу из указанной
разности (сам i-ый отрезок не считаем),
получим количество отрезков, с которыми i-ый
отрезок имеет хотя бы
одну общую точку.
for(i = 0; i
< n; i++)
{
res = upper_bound(alLeft, alLeft + n,
right[i]) - alLeft;
res -= lower_bound(alRight, alRight + n,
left[i]) - alRight;
printf("
%d",res - 1);
}
printf("\n");
}