5187. Point of heights intersection

Find the intersection point of heights for given triangle.

Input. The coordinates of the three vertices of triangle (first the coordinates of the first vertex, then the second, then the third). Coordinates are the pair of integers not exceeding 10⁴ in absolute value.

Output. Print two numbers – the coordinates of intersection point for triangle heights with an accuracy of at least 6 decimal digits.

Sample input	Sample output
0 0 3 0 0 4	0.0 0.0

SOLUTION

geometry

Algorithm analysis

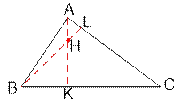
Let A(x_a, y_a), B(x_b, y_b), C(x_c, y_c) be three triangle vertices. Draw the heights AK and BL. The point of their intersection H will be the desired one.

Write the equation of the line AK: it must pass through the vertex A and be perpendicular to the line BC. Let the equation of the line AK have the form a₁x + b₁y = c₁. Then the vector (a₁, b₁) coincides with the direction of the vector BC and we can put (a₁, b₁) = (x_c – x_b, y_c – y_b). Equation of the line AK has the form

(x_c – x_b)x + (y_c – y_b)y = c₁

Since line AK passes through point A, substituting the coordinates of point A(x_a, y_a) into its equation, we find the value of c₁:

(x_c – x_b) x_a + (y_c – y_b) y_a = c₁

Similarly find the equation of the line BL. Let it has the form a₂x + b₂y = c₂. The vector (a₂, b₂) coincides with the direction of the vector AC and we can put (a₂, b₂) = (x_c – x_a, y_c – y_a). Point B lies on line BL, hence

(x_c – x_a) x_b + (y_c – y_a) y_b = c₂

The intersection point of the heights of triangle can be found by solving the system of equations

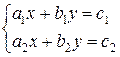
with Kramer’s method.

Algorithm realization

Function kramer finds the solution (x, y) of system of equations

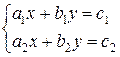
void kramer(double a1, double b1, double c1,

double a2, double b2, double c2, double &x, double &y)

{

double d = a1 * b2 - a2 * b1;

double dx = c1 * b2 - c2 * b1;

double dy = a1 * c2 - a2 * c1;

x = dx / d; y = dy / d;

}

Read the input data.

scanf("%lf %lf %lf %lf %lf %lf",&xa,&ya,&xb,&yb,&xc,&yc);

Find the equation of the line AK: a₁x + b₁y = c₁.

a1 = xc - xb;

b1 = yc - yb;

c1 = xa * (xc - xb) + ya * (yc - yb);

Find the equation of the line BL: a₂x + b₂y = c₂.

a2 = xc - xa;

b2 = yc - ya;

c2 = xb * (xc - xa) + yb * (yc - ya);

Find and print the intersection point of the triangle heights.

kramer(a1,b1,c1,a2,b2,c2,x,y);

printf("%.6lf %.6lf\n",x,y);

Java realization

import java.util.*;

public class Main

{

static double[] kramer(double a1, double b1, double c1,

double a2, double b2, double c2)

{

double res[] = new double[2]; // x, y

double d = a1 * b2 - a2 * b1;

double dx = c1 * b2 - c2 * b1;

double dy = a1 * c2 - a2 * c1;

res[0] = dx / d;

res[1] = dy / d;

return res;

}

public static void main(String []args)

{

Scanner con = new Scanner(System.in);

double xa = con.nextDouble();

double ya = con.nextDouble();

double xb = con.nextDouble();

double yb = con.nextDouble();

double xc = con.nextDouble();

double yc = con.nextDouble();

double a1 = xc - xb;

double b1 = yc - yb;

double c1 = xa * (xc - xb) + ya * (yc - yb);

double a2 = xc - xa;

double b2 = yc - ya;

double c2 = xb * (xc - xa) + yb * (yc - ya);

double res[] = kramer(a1,b1,c1,a2,b2,c2);

System.out.println(res[0] + " " + res[1]);

con.close();

}

}