5190. Construct a triangle with two sides and the included angle

Construct a triangle given two sides and included angle.

Input. Contains three real numbers – the lengths of two sides of triangle and the angle between them in degrees. The lengths of the sides are positive numbers not exceeding 10⁴, the angle is a positive number less than 180.

Output. Print 6 real numbers – the coordinates of the vertices of any triangle corresponding to the given input data with an accuracy at least 6 decimal digits.

Sample input	Sample output
10 5 60	0 0 10.0 0 2.5000000000 4.3301270189

SOLUTION

geometry

Algorithm analysis

Let A, B, C be three vertices of triangle, BC = a, AC = b. Place the origin of the coordinate system (0, 0) at point C, direct the abscissa axis along the vector CB. Then point B has coordinates (a, 0).

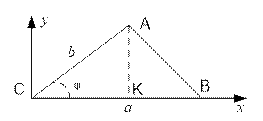
Draw the height AK. From tringle CAK: AK = AC sin φ, CK = AC cos φ. Considering that AC = b, point А will have coordinates (b cos φ, b sin φ).

Algorithm realization

Declare the constant π.

#define PI acos(-1.0)

Read the input data.

scanf("%lf %lf %lf",&a,&b,&fi);

Convert angle fi to radians.

fi = fi / 180 * PI;

Print the coordinates of three points.

printf("%.6lf %.6lf\n",0,0);

printf("%.6lf %.6lf\n",a,0);

printf("%.6lf %.6lf\n",b*cos(fi),b*sin(fi));

Java realization

import java.util.*;

public class Main

{

static double[] kramer(double a1, double b1, double c1,

double a2, double b2, double c2)

{

double res[] = new double[2]; // x, y

double d = a1 * b2 - a2 * b1;

double dx = c1 * b2 - c2 * b1;

double dy = a1 * c2 - a2 * c1;

res[0] = dx / d;

res[1] = dy / d;

return res;

}

public static void main(String []args)

{

Scanner con = new Scanner(System.in);

double a = con.nextDouble();

double b = con.nextDouble();

double fi = con.nextDouble();

fi = fi / 180 * Math.PI;

System.out.println("0 0");

System.out.println(a + " " + 0);

System.out.println(b * Math.cos(fi) + " " + b * Math.sin(fi));

con.close();

}

}