5205. Скобки

Задан шаблон, состоящий из круглых скобок и знаков вопроса.

Определить, сколькими способами можно заменить знаки вопроса круглыми скобками так, чтобы получилось правильная скобочная последовательность.

Вход. Первая строка содержит заданный шаблон длиной не более 2000 символов.

Выход. Выведите искомое количество способов по модулю 301907.

Пример входа	Пример выхода
????(?	2

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Пусть f(n, k) равно количеству правильных скобочных записей, начинающихся с позиции n, если до этого уже встретилось k открытых скобок. Тогда ответом задачи будет значение f(0, 0). Значение f(n, k) сохраняем в dp[n][k].

Пусть s – входная строка. Тогда:

· если s[n] = ‘(‘, то f(n, k) = f(n + 1, k + 1). До позиции n будет k открытых скобок, если до позиции n + 1 будет k + 1 открытая скобка;

· если s[n] = ‘)‘, то f(n, k) = f(n + 1, k – 1) . До позиции n будет k открытых скобок, если до позиции n + 1 будет k – 1 открытая скобка;

· если s[n] = ‘?‘, то на n-ом месте можно поставить как открывающую, так и закрывающую скобку. Поэтому f(n, k) = (f(n + 1, k + 1) + f(n + 1, k – 1)) % 301907;

Осталось записать условия окончания динамики:

· если на некотором этапе станет k < 0, то количество закрытых скобок оказывается больше числа открытых, поэтому выходим из этой ветки вычислений, возвращаем 0;

· если дошли до конца строки s₀s₁ … s_n-1 (нумерация индексов начинается с нуля), то dp[n][k] = 1 если только k = 0 (когда число открытых и закрытых скобок одинаково). При k > 0 положим dp[n][k] = 0.

Пример

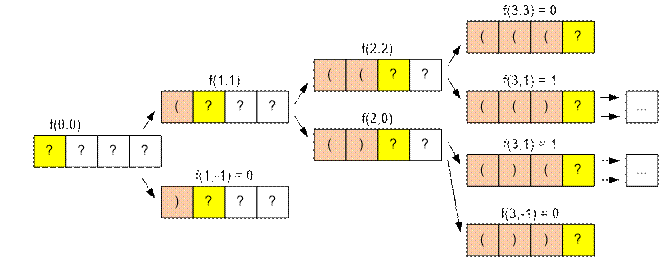
Реализация алгоритма

Объявим рабочие массивы.

#define MAX 2010

char s[MAX];

int dp[MAX][MAX];

int len;

Реализация функции f(n, k).

int f(int n, int k)

{

if(k < 0) return 0;

if(n == len) return (k == 0);

if(dp[n][k] != -1) return dp[n][k];

if(s[n] == '(') return dp[n][k] = f(n+1, k+1);

if(s[n] == ')') return dp[n][k] = f(n+1, k-1);

return dp[n][k] = (f(n+1, k-1) + f(n+1, k+1)) % 301907;

}

Основная часть программы. Читаем строку и выводим количество искомых правильных скобочных записей.

gets(s); len = strlen(s);

memset(dp,-1,sizeof(dp));

printf("%d\n",f(0,0));

Java реализация

import java.util.*;

public class Main

{

static String s;

static int dp[][];

static int f(int n, int k)

{

if(k < 0) return 0;

if(n == s.length()) return (k == 0) ? 1 : 0;

if(dp[n][k] != -1) return dp[n][k];

if(s.charAt(n) == '(') return dp[n][k] = f(n+1, k+1);

if(s.charAt(n) == ')') return dp[n][k] = f(n+1, k-1);

return dp[n][k] = (f(n+1, k-1) + f(n+1, k+1)) % 301907;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

s = con.next();

int len = s.length();

dp = new int[len ][len ];

for(int i = 0; i < len; i++)

Arrays.fill(dp[i], -1);

System.out.println(f(0,0));

con.close();

}

}