5205. Mötərizələr
Yumru
mötərizə və sual işarələrindən
ibarət şablon verilir
Syal
işarələrini dəyişməklə neçə
müxtəlif üsulla düzgün mötərizə
ifadəsi almaq olar
Giriş. Birinci
sətirdə, uzunluğu 2000-i aşmayan şablon verilir.
Çıxış. Axtarılan
üsulların sayını 301907 moduluna görə
çıxarın..
Girişə
nümunə
????(?
Çıxışa
nümunə
2
Həlli
dinamik proqramlama
Alqoritmin analizi
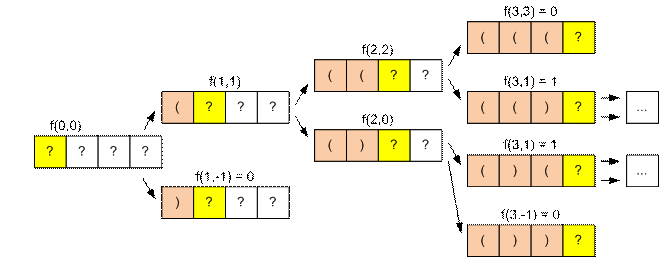
Tutaq ki, f(n, k) - artıq k sayda açılan mötərizə olubsa onda n -ci mövqedən başlayan, düzgün mötərizə
ifadələrinin sayına bərabərdir. Onda
məsələnin cavabı f(0, 0) olar. f(n, k) –nın
qiymətini dp[n][k].-da saxlayırıq
Tutaq ki, s – giriş
sətridir. Onda:
·
əgər s[i] = ‘(‘,
isə
f(n, k) = f(n + 1, k + 1);
·
əgər s[i] = ‘)‘,
isə f(n, k) = f(n + 1, k – 1);
·
əgər s[i] = ‘?‘,
isə i-ci yerə açılan
mötərizə də qoymaq olar bağlanan
mötərizə də. Odur ki. f(n, k) = (f(n + 1, k + 1) + f(n + 1, k – 1)) % 301907;
İndi dinamikanın
bitmə şərtini yazmaq qalır.
·
Əgər hansı etapda isə k < 0 olarsa, bu hesablama nahiyəsindən çıxaraq
çıxışa 0 veririk;
·
Əgər s0s1 … sn-1 sətrinin sonuna çatdıqsa (indeksləri
nömrələmə 0 –dan başlayır), onda dp[n][k] = 1 əgər k = 0 olarsa. k > 0 halında dp[n][k] = 0.
Alqoritmin
realizə olunması
İşçi massivləri təyin edək:
#define MAX 2010
char s[MAX];
int dp[MAX][MAX];
int len;
f(n, k).funksiyasını
işə salırıq
int f(int
n, int k)
{
if(k < 0) return 0;
if(n == len) return (k == 0);
if(dp[n][k]
!= -1) return dp[n][k];
if(s[n]
== '(')
return
dp[n][k] = f(n+1, k+1);
if(s[n]
== ')')
return dp[n][k] = f(n+1, k-1);
return
dp[n][k] = (f(n+1, k-1) + f(n+1, k+1)) % 301907;
}
Proqramın əsas hissəsi. Sətri oxuyur və axtarılan düzgün
mötərizə ifadəsinin sayını
çıxarırıq.
gets(s); len =
strlen(s);
memset(dp,-1,sizeof(dp));
printf("%d\n",f(0,0));