5213. Inverse
Prime number n is given. The inverse number to i (1 ≤ i < n) is such number j that i * j = 1 (mod n). It’s possible to prove
that for each i exists only one
inverse.
For all possible
values of i find the
inverse numbers.
Input. One prime number n (2 ≤ n ≤ 106).
Output. Print n – 1 numbers. The i-th printed
number should be the inverse to i.
|
Sample
input |
Sample
output |
|
5 |
1 3 2 4 |
SOLUTION
exponentiation
Algorithm analysis
Since the number n is prime, then by Fermat’s theorem in-1 mod n = 1 for every 1 ≤ i < n. This equality can be rewritten in the form (i * in-2)
mod n = 1, whence the inverse of i equals to j = in-2
mod n.
The inverse can be found using the extended
Euclidean algorithm. Let the the modulo equation should be solved: ax = 1 (mod n). Consider the
equation
ax + ny = 1
and find its partial
solution (x0, y0) using the extended
Euclidean algorithm. Taking the equation ax0 + ny0 = 1 modulo n, we get ax0
= 1 (mod n). If x0 is negative, add n to it. So x0 = a-1 (mod n) is
the inverse for a.
In both algorithms, for
each i (1 ≤ i < n) we searched for the inverse in O(log2n). Thus, the complexity
of the whole algorithm is O(n log2n).
Consider the O(n)
solution.
Theorem. If inv[i] is the
inveerse of i modulo n, then
inv[i] =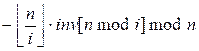 
Proof. It is known that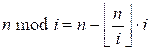 
Take modulo n both sides: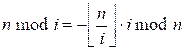 
Multiply both sides by i-1 * (n mod i) -1:
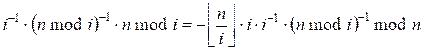
After
simplification, we get:
According to the
formula given in the theorem, the value of inv[i] for each i (1 ≤ i < n) can be found in
O(1) time. Thus, all inverse elements will be found in O(n).
Example
Let n = 5. Consider the table:
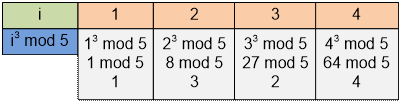
Let’s find the inverse elements using the
formula from the theorem:
inv[1] = 1 (the base case)
inv[2] = 
= (-2 ∙ inv[1]) mod 5 = -2 mod
5 = 3
inv[3] =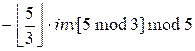 
= (-1 ∙ inv[2]) mod 5 = -3 mod 5 = 2
inv[4] = 
= (-1 ∙ inv[1]) mod 5 = -1 mod 5 = 4
Algorithm realization
Function
Pow
returns the value of xn mod m.
long long
Pow(long long
x, long long n,
long long m)
{
if (n == 0) return 1;
if (n % 2 ==
0) return Pow((x * x) % m, n / 2, m);
return (x *
Pow(x, n - 1, m)) % m;
}
The
main part of the program. Read the
input value of n.
scanf("%d",&n);
For each number i print the corresponding to it inverse number in-2 mod n.
for(i = 1; i < n; i++)
printf("%lld
",Pow(i,n-2,n));
printf("\n");
Algorithm realization – extended Euclidean algorithm
#include <stdio.h>
int n, i, d, x, y;
void gcdext(int a, int b, int &d, int &x, int &y)
{
if (b == 0)
{
d = a; x
= 1; y = 0;
return;
}
gcdext(b,
a % b, d, x, y);
int s = y;
y = x -
(a / b) * y;
x = s;
}
int main(void)
{
scanf("%d", &n);
for (i = 1; i < n; i++)
{
// i * x
+ n * y = 1
gcdext(i,
n, d, x, y);
if (x < 0) x += n;
printf("%d ", x);
}
printf("\n");
return 0;
}
Algorithm realization – O(n)
Declare an array inv in which we’ll compute the
inverse elements.
inv[i] = i-1
mod n.
#define MAX 1000001
int inv[MAX];
Read the
input value of n.
scanf("%d", &n);
Compute the
inverse elements according to the formula.
inv[1] = 1;
for (i = 2; i <= n; i++)
inv[i] = n - 1LL * (n / i) * inv[n % i] % n;
Print the
answer.
for (i = 1; i < n; i++)
printf("%d
", inv[i]);
Java realization
import java.util.*;
public class Main
{
static long PowMod(long x, long n, long m)
{
if (n == 0) return 1;
if (n % 2 == 0) return PowMod((x * x) % m, n / 2, m);
return (x * PowMod(x, n - 1, m)) % m;
}
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
long n = con.nextLong();
for(int i = 1; i < n; i++)
System.out.print(PowMod(i,n-2,n) + " ");
System.out.println();
con.close();
}
}
Java realization – linear solution
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int inv[] = new int[n];
inv[1] = 1;
for (int i = 2; i < n; i++)
inv[i] = (int) (n - 1L * (n / i) * inv[n % i] % n);
for(int i = 1; i < n; i++)
System.out.print(inv[i] + " ");
System.out.println();
con.close();
}
}
Python realization – linear
solution
n = int(input())
inv = [0 for _ in range(n + 1)]
inv[1] = 1;
for i in range(2,n):
inv[i] = n - (n // i) * inv[n % i] % n;
for i in range(1,n):
print(inv[i], end= " ")