5290. Подстроки (Easy)

Дана строка s. Подсчитайте количество её различных подстрок. Пустую строку учитывать не следует.

Вход. Одна строка s, состоящая из строчных латинских букв. Длина строки не превосходит 100 символов.

Выход. Выведите одно число – количество различных подстрок s.

Пример входа	Пример выхода
abacaba	21

РЕШЕНИЕ

структуры данных – бор

Анализ алгоритма

Занесем все суффиксы строки s в бор. Количество вершин в боре будет равняться числу различных подстрок s с учетом пустой подстроки.

Пример

Бор, построенный изо всех суффиксов слова abacaba, имеет вид:

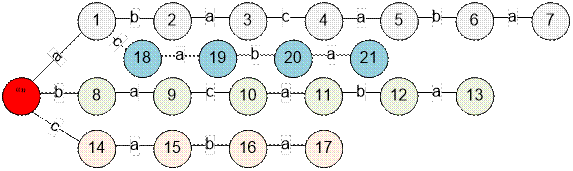
Бор содержит 21 вершину не считая начальную (которой соответствует пустое слово).

Реализация алгоритма

Структура вершины бора.

struct node

{

int next[26];

node()

{

for(int i = 0; i < 26; i++) next[i] = 0;

}

};

Объявим бор. Сначала он состоит из одной вершины.

vector<node> trie(1);

Читаем входную строку.

gets(s); len = strlen(s);

Заносим все суффиксы строки s в бор.

for(i = 0; i < len; i++)

{

pos = 0;

Заносим в бор суффикс s_i s_i+1 …s_len-1.

for(j = i; j < len; j++)

{

char ch = s[j] - 'a';

if (trie[pos].next[ch] == 0)

{

node temp;

trie[pos].next[ch] = trie.size();

trie.push_back(temp);

}

pos = trie[pos].next[ch];

}

}

Выводим количество разных подстрок. Оно на единицу меньше числа вершин в боре (пустая подстрока не считается).

printf("%d\n",trie.size() - 1);