5306. Камни

На столе лежат n камней. Играют двое, ходят по очереди. За ход игрок может взять:

· 1 или 2 камня, если n делится на 3;

· 1 или 3 камня, если дает остаток 1;

· 1, 2 или 3 камня, если дает остаток 2.

Каждый ход можно сделать только при наличии достаточного количества камней. Проигрывает тот, кто хода сделать не может.

Вход. Одно целое число n (0 < n ≤ 100).

Выход. Выведите одно число 1 или 2 – номер игрока, который выигрывает при правильной игре.

Пример входа	Пример выхода
3	2

РЕШЕНИЕ

теория игр

Анализ алгоритма

Вычислим в линейном массиве выигрышные и проигрышные позиции:

· ноль камней – проигрышная позиция (совершить ход невозможно);

· один или два камня – выигрышная позиция (забираем все имеющиеся камни и соперник не может совершить ход);

Если из текущей позиции можно совершить хода только в выигрышные позиции, то текущая позиция – проигрышная. Иначе – выигрышная.

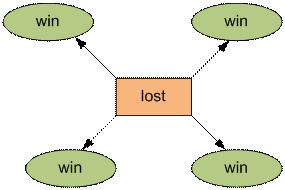
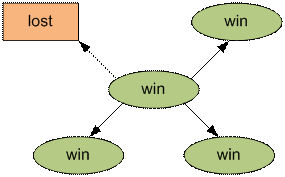
По такому принципу последовательно вычисляем выигрышность каждой позиции от 0 до n.

Проигрышными будут состояния, в которых n кратно 3. Действительно, пусть n делится на 3. Тогда независимо от хода игрока второй игрок всегда может сделать ход так, чтобы после него число камней в кучке снова делилось на 3.

Реализация алгоритма

Информацию о выигрышных и проигрышных позициях храним в массиве m.

#define MAX 1001

int m[MAX];

Проигрышные позиции кодируем единицей, выигрышные – нулем.

m[0] = 1; // Lost

m[1] = m[2] = 0; // Win

Читаем имеющееся количество камней на столе.

scanf("%d",&n);

Вычисляем значения всех позиций (проигрышные или выигрышные).

for(i = 3; i <= n; i++)

{

if (i % 3 == 0)

{

s = m[i-1] + m[i-2];

if (s > 0) m[i] = 0; else m[i] = 1;

} else

if (i % 3 == 1)

{

s = m[i-1] + m[i-3];

if (s > 0) m[i] = 0; else m[i] = 1;

}

else

{

s = m[i-1] + m[i-2] + m[i-3];

if (s > 0) m[i] = 0; else m[i] = 1;

}

}

В зависимости от значения m[n] выводим ответ.

if (m[n]== 1) printf("2\n"); else printf("1\n");