5327. Bracket sequence
The bracket
sequence is a correct arithmetic expression from which all numbers and operation
signs have been removed. For example,
1 + ( ( ( 2 + 3 ) + 5 ) + ( 3 + 4 ) ) → ( ( ( ) ) ( ) )
Input. A sequence of opening and closing brackets
is given. The length of the sequence is no more than 4 * 106.
Output. Print “YES” if the bracket sequence is correct and “NO” otherwise.
|
Sample
input 1 |
Sample
output 1 |
|
((())()) |
YES |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
(() |
NO |
SOLUTION
stack
Algorithm analysis
Let’s declare a
stack in which we will store only opening brackets. Upon receiving each
character, we perform the following operation with the stack:
·
if the character ‘(‘ is encountered, we push
it onto the stack;
·
if the character ‘)’ is encountered, we pop
an element from the stack.
If the stack is empty at this point, the sequence is not a bracket sequence (at
some point, the number of closing brackets exceeds the number of opening brackets);
At the end of
processing
the string, the stack should be empty.
We can simulate the stack using
a single variable. Let the variable cnt store the
number of open brackets in the stack. Then, when pushing ‘(‘ onto the stack, we perform the operation
cnt++, and when removing an
element from the
stack,
we perform the operation cnt--.
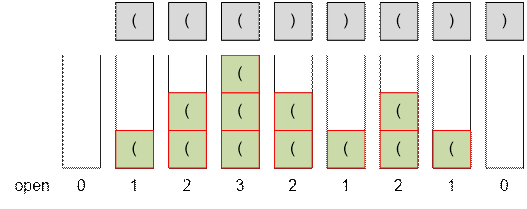
Example
Let’s simulate the stack operations
for the string “((())())” from the first example.
Algorithm implementation
Read the input string.
cin >> s;
The variable cnt stores the number of current unclosed brackets (i.e., the number of
opening brackets for which corresponding closing
brackets have not yet been encountered).
The variable flag will be set to
1 if, at any iteration, the number of closing brackets exceeds
the number of opening brackets. Initially, we set flag = 0.
cnt = flag = 0;
Process the input
string character by character, simulating stack operations.
for (i = 0; i < s.size(); i++)
{
Process the current character s[i].
if (s[i] == '(') cnt++; else cnt--;
If the number of closing brackets exceeds
the number of opening brackets at any iteration, then the input sequence is not a bracket sequence.
if (cnt < 0) flag =
1;
}
Depending on the values of the
variables flag
and cnt, print the answer. The stack will be
empty at the end of processing the string if cnt = 0.
if (flag ==
0 && cnt == 0)
cout << "YES\n"; else cout << "NO\n";
Java implementation – string
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
String s = con.nextLine();
boolean flag = false;
int open = 0;
for(int i = 0; i < s.length(); i++)
{
if (s.charAt(i) == '(')
open++;
else
open--;
if (open < 0)
flag = true;
}
if (flag || (open > 0))
System.out.println("NO");
else
System.out.println("YES");
con.close();
}
}
Java implementation – char array
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner
con = new Scanner(System.in);
char s[] = con.nextLine().toCharArray();
boolean flag = false;
int open = 0;
for(int i = 0; i < s.length; i++)
{
if (s[i] == '(')
open++;
else
open--;
if (open < 0)
flag = true;
}
if (flag || (open > 0))
System.out.println("NO");
else
System.out.println("YES");
con.close();
}
}
Python implementation
Read the input string.
s = input()
The variable cnt stores the number of current unclosed brackets (i.e., the number of
opening brackets for which corresponding closing
brackets have not yet been encountered).
The variable flag will be set to
1 if, at any iteration, the number of closing brackets exceeds
the number of opening brackets. Initially, we set flag = 0.
cnt = flag = 0
Process the input
string character by character, simulating stack operations.
for ch in s:
Process the current character ch.
if ch == '(': cnt += 1
else: cnt -= 1
If the number of closing brackets exceeds
the number of opening brackets at any iteration, then the input sequence is not a bracket sequence.
if cnt < 0: flag = 1
Depending on the values of the
variables flag
and cnt, print the answer. The stack will be
empty at the end of processing the string if cnt = 0.
if flag == 0 and cnt == 0:
print("YES")
else:
print("NO")