5329. Вечерка

Сколькими способами среди n ЛКШат можно выбрать k таких, которым достанется кефир? Ответ выведите по модулю 9929.

Вход. Целые числа n и k (0 ≤ k ≤ n ≤ 500).

Выход. Выведите искомое количество способов по модулю 9929.

Пример входа	Пример выхода
6 3	20

РЕШЕНИЕ

комбинаторика – биномиальный коэффициент

Анализ алгоритма

Ответом к задаче будет значение . Поскольку следует найти биномиальный коэффициент по модулю, постараемся при вычислениях избежать деления. Для этого воспользуемся соотношением = + , = 1.

Задачу можно решить также по формуле

= = ,

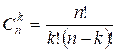заменив деление умножением на обратное число по модулю 9929. Отметим, что число 9929 простое. То есть n / i = n * (i^-1) mod 9929.

По теореме Ферма i⁹⁹²⁸ mod 9929 = 1 или (i * i⁹⁹²⁷) mod 9929 = 1, откуда обратным к i по модулю 9929 будет i⁹⁹²⁷ mod 9929. Таким образом

(i^-1) mod 9929 = i⁹⁹²⁷ mod 9929

Реализация алгоритма

Объявим константы и массив cnk, для которого cnk[n][k] = .

#define MAX 510

#define MOD 9929

int cnk[MAX][MAX];

Функция c вычисляет значение биномиального коэффициента .

int c(int n, int k)

{

if (cnk[n][k] > 0) return cnk[n][k];

if (n - k < k) return c(n,n-k);

if (!k) return cnk[n][k] = 1;

return cnk[n][k] = (c(n-1,k) + c(n-1,k-1)) % MOD;

}

Основная часть программы. Инициализируем массив cnk нулями. Читаем входные данные.

memset(cnk,0,sizeof(cnk));

scanf("%d %d",&n,&k);

Вычисляем и выводим ответ.

printf("%d\n",c(n,k));

Реализация алгоритма – циклическая

Объявим константы и массив cnk, для которого cnk[n][k] = .

#define MAX 502

#define MOD 9929

int cnk[MAX][MAX];

Функция FillCnk заполняет массив cnk биномиальными коэффициентами.

void FillCnk(void)

{

int n, k;

memset(cnk,0,sizeof(cnk));

Инициализация cnk[n][0] = = 1.

for(n = 0; n < MAX; n++) cnk[n][0] = 1;

Проводим вычисления, воспользовавшись формулой = + . Вычисления проводим по модулю MOD.

for(n = 1; n < MAX; n++)

for(k = 1; k <= MAX; k++)

cnk[n][k] = (cnk[n-1][k] + cnk[n-1][k-1]) % MOD;

}

Основная часть программы. Заполняем массив биномиальных коэффициентов.

FillCnk();

Читаем входные данные. Вычисляем и выводим ответ.

scanf("%d %d",&n,&k);

printf("%d\n",cnk[n][k]);

Реализация алгоритма – обратное по модулю

Функция pow вычисляет xⁿ mod p.

int pow(int x, int n, int p)

{

if (n == 0) return 1;

if (n % 2 == 0) return pow((x * x) % p, n / 2, p);

return (x * pow(x, n - 1, p)) % p;

}

Функция inverse вычисляет число, обратное x, по модулю p: x^-1 mod p (p простое).

int inverse(int x, int p)

{

return pow(x, p - 2, p);

}

Функция Cnk вычисляет значение биномиального коэффициента по модулю p. Для этого выражение

res = res * (n – i + 1) / i

перепишем в виде

res = (res * (n – i + 1) * (i^-1 mod p)) mod p

int Cnk(int n, int k, int p)

{

int res = 1;

if (k > n - k) k = n - k;

for (int i = 1; i <= k; i++)

res = ((res * (n - i + 1)) % p * inverse(i, p)) % p;

return res;

}

Основная часть программы. Читаем входные данные.

scanf("%d %d", &n, &k);

Вычисляем и выводим ответ.

res = Cnk(n, k, 9929);

printf("%d\n", res);

Java реализация

import java.util.*;

public class Main

{

static int dp[][];

static int MOD = 9929;

static int Cnk(int n, int k)

{

if (n == k) return 1;

if (k == 0) return 1;

if (dp[n][k] != -1) return dp[n][k];

return dp[n][k] = (Cnk(n - 1, k - 1) + Cnk(n - 1, k)) % MOD;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int k = con.nextInt();

dp = new int[n+1][k+1];

for(int i = 0; i <= n; i++)

Arrays.fill(dp[i],-1);

int res = Cnk(n,k);

System.out.println(res);

con.close();

}

}

Java реализация – итерационная, длинная арифметика

import java.util.*;

import java.math.*;

public class Main

{

static BigInteger Cnk(int n, int k)

{

BigInteger res = BigInteger.ONE;

BigInteger MOD = BigInteger.valueOf(9929);

BigInteger p = BigInteger.valueOf(n);

BigInteger q = BigInteger.valueOf(1);

for (int i = 0; i < k; i++)

{

res = res.multiply(p).multiply(q.modInverse(MOD)).mod(MOD);

p = p.subtract(BigInteger.ONE);

q = q.add(BigInteger.ONE);

}

return res;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int k = con.nextInt();

BigInteger res = Cnk(n,k);

System.out.println(res);

con.close();

}

}

Python реализация

Функция Cnk вычисляет значение биномиального коэффициента и запоминает его значение в ячейке dp[n][k].

def Cnk(n, k, dp):

if n == k: return 1

if k == 0: return 1

if dp[n][k] != -1: return dp[n][k]

dp[n][k] = (Cnk(n - 1, k - 1, dp) + Cnk(n - 1, k, dp)) % 9929

return dp[n][k]

Основная часть программы. Читаем входные данные.

n, k = map(int, input().split())

Инициализируем двумерный список для запоминания значений:

dp[x][y] =

dp = [[-1] * 501 for _ in range(501)]

Вычисляем и выводим ответ.

print(Cnk(n, k, dp))