5329. Party

 

How many ways are there to choose k out of n participants in the summer math camp, each of whom will receive kefir? Print the answer modulo 9929.

 

Input. Two integers n and k (0 ≤ k ≤ n ≤ 500).

 

Output. Print the number of ways modulo 9929.

 

Sample input

Sample output

6 3

20

 

 

SOLUTION

combinatorics – binomial coefficient

 

Algorithm analysis

The answer to the problem will be the value of . Since we need to find the binomial coefficient by modulo, we’ll try to avoid division during calculations. To achieve this, use the relation:  =  + ,  = 1.

 

The problem can also be solved using the formula:

 =  = ,

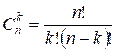by replacing division with multiplication by the inverse number modulo 9929. Note that the number 9929 is a prime. That is, n / i = n * (i-1) mod 9929.

According to Fermat’s theorem, i9928 mod 9929 = 1 or (i * i9927) mod 9929 = 1, hence the inverse of i modulo 9929 will be i9927 mod 9929. Thus,

(i-1) mod 9929 = i9927 mod 9929

 

Algorithm realization

Declare the constants and array cnk, where cnk[n][k] = .

 

#define MAX 510

#define MOD 9929

int cnk[MAX][MAX];

 

The c function computes the value of the binomial coefficient .

 

int c(int n, int k)

{

  if (cnk[n][k] > 0) return cnk[n][k];

  if (n - k < k) return c(n,n-k);

  if (!k) return cnk[n][k] = 1;

  return cnk[n][k] = (c(n-1,k) + c(n-1,k-1)) % MOD;

}

 

The main part of the program. Initialize the cnk array with zeros. Read the input data.

 

memset(cnk,0,sizeof(cnk));

scanf("%d %d",&n,&k);

 

Compute and print the answer.

 

printf("%d\n",c(n,k));

 

Algorithm realization – loops

Declare the constants and array cnk, where cnk[n][k] = .

 

#define MAX 502

#define MOD 9929

int cnk[MAX][MAX];

 

The FillCnk function fills the cnk array with binomial coefficients.

 

void FillCnk(void)

{

  int n, k;

  memset(cnk,0,sizeof(cnk));

 

Initialize cnk[n][0] =  = 1.

 

  for(n = 0; n < MAX; n++) cnk[n][0] = 1;

 

Perform the computation using the formula  =  +  modulo MOD.

 

  for(n = 1; n < MAX; n++)

  for(k = 1; k <= MAX; k++)

    cnk[n][k] = (cnk[n-1][k] + cnk[n-1][k-1]) % MOD;

}

 

The main part of the program. Fill the array of binomial coefficients.

 

FillCnk();

 

Read the input data. Compute and print the answer.

 

scanf("%d %d",&n,&k);

printf("%d\n",cnk[n][k]);

 

Algorithm realization – inverse modulo

The pow function computes xn mod p.

 

int pow(int x, int n, int p)

{

  if (n == 0) return 1;

  if (n % 2 == 0) return pow((x * x) % p, n / 2, p);

  return (x * pow(x, n - 1, p)) % p;

}

 

The inverse function computes the number that is the inverse of x modulo p: x-1 mod p (where p is prime).

 

int inverse(int x, int p)

{

  return pow(x, p - 2, p);

}

 

The Cnk function computes the value of the binomial coefficient  modulo p. To achieve this, rewrite an expression

res = res * (n – i + 1) / i

in the form

res = (res * (n – i + 1) * (i-1 mod p)) mod p

 

int Cnk(int n, int k, int p)

{

  int res = 1;

  if (k > n - k) k = n - k;

  for (int i = 1; i <= k; i++)

    res = ((res * (n - i + 1)) % p * inverse(i, p)) % p;

  return res;

}

 

The main part of the program. Read the input data.

 

scanf("%d %d", &n, &k);

 

Compute and print the answer.

 

res = Cnk(n, k, 9929);

printf("%d\n", res);

 

Java realization

 

import java.util.*;

 

public class Main

{

  static int dp[][];

  static int MOD = 9929;

 

  static int Cnk(int n, int k)

  {

    if (n == k) return 1;

    if (k == 0) return 1;

    if (dp[n][k] != -1) return dp[n][k];

    return dp[n][k] = (Cnk(n - 1, k - 1) + Cnk(n - 1, k)) % MOD;

  }

  public static void main(String[] args)

  {

    Scanner con = new Scanner(System.in);

    int n = con.nextInt();

    int k = con.nextInt();

    dp = new int[n+1][k+1];

    for(int i = 0; i <= n; i++)

      Arrays.fill(dp[i],-1);

   

    int res = Cnk(n,k);

    System.out.println(res);

    con.close();

  }

}

 

Java realization – loops, long arithmetic

 

import java.util.*;

import java.math.*;

 

public class Main

{

  static BigInteger Cnk(int n, int k)

  {

    BigInteger res = BigInteger.ONE;

    BigInteger MOD = BigInteger.valueOf(9929);

    BigInteger p = BigInteger.valueOf(n);

    BigInteger q = BigInteger.valueOf(1);

    for (int i = 0; i < k; i++)

    {

      res = res.multiply(p).multiply(q.modInverse(MOD)).mod(MOD);

      p = p.subtract(BigInteger.ONE);

      q = q.add(BigInteger.ONE);

    }

    return res;

  }

 

  public static void main(String[] args)

  {

    Scanner con = new Scanner(System.in);

    int n = con.nextInt();

    int k = con.nextInt();

         

    BigInteger res = Cnk(n,k);

    System.out.println(res);

    con.close();

  }

}

 

Python realization

The Cnk function computes the value of the binomial coefficient  and memoizes its value in the cell dp[n][k].

 

def Cnk(n, k, dp):

  if n == k: return 1

  if k == 0: return 1

  if dp[n][k] != -1: return dp[n][k]

  dp[n][k] = (Cnk(n - 1, k - 1, dp) + Cnk(n - 1, k, dp)) % 9929

  return dp[n][k]

 

The main part of the program. Read the input data.

 

n, k = map(int, input().split())

 

Initialize a two-dimensional list for memoizing the values:

dp[x][y] =

 

dp = [[-1] * 501 for _ in range(501)]

 

Compute and print the answer.

 

print(Cnk(n, k, dp))