5363. Сушка
Стирать бельё
зимой – задача не из
простых, а сушить его ещё сложнее. Но Джейн – сообразительная девочка и не
боится рутинных дел. Чтобы ускорить процесс сушки, она решила воспользоваться
радиатором. Однако радиатор небольшой и в каждый момент времени может сушить
только одну вещь.
Джейн хочет
высушить бельё как можно быстрее. Она просит Вас написать программу, которая
определит минимальное время, необходимое для сушки всего набора одежды.
Джейн только что
постирала n вещей. Во время стирки каждая вещь впитала ai единиц воды. С каждой
минутой количество воды в каждой вещи уменьшается на одну единицу (если вещь
ещё не высохла). Как только количество воды становится равным нулю, вещь
считается сухой и готова к упаковке.
Кроме того,
каждую минуту Джейн может выбрать одну вещь и положить её на радиатор. Радиатор
достаточно горячий, поэтому вещь на нём теряет k единиц воды за минуту
(но не более, чем содержится воды: если в вещи меньше k единиц воды, она
просто полностью высыхает за эту минуту).
Ваша задача – определить
минимальное количество времени, необходимое для сушки всей одежды при
оптимальном использовании радиатора. Сушка считается завершённой, когда вся
одежда становится сухой.
Вход. Первая строка содержит одно целое число n (1 ≤ n ≤ 105) – количество вещей.
Вторая строка содержит n целых чисел ai (1 ≤ ai ≤ 109), где ai – количество воды в i-ой вещи после стирки.
Третья строка содержит одно целое число k (1 ≤ k ≤ 109)
– скорость
испарения воды с вещи, лежащей на радиаторе (в единицах воды в минуту).
Выход. Выведите одно число – наименьшее количество минут, необходимое для полной
сушки всех вещей.
|
Пример
входа |
Пример
выхода |
|
3 2 3 9 5 |
3 |
РЕШЕНИЕ
бинарный
поиск
Анализ алгоритма
Пусть max – наибольшее значение среди всех ai. Очевидно, что через max минут все белье высохнет самостоятельно, даже без
использования радиатора.
Пусть ответом
является значение m. Это означает, что всё
бельё, содержащее не более m единиц воды, успеет высохнуть естественным
образом. А вещи, в которых воды больше m, необходимо дополнительно
сушить на радиаторе.
Будем считать, что каждое
бельё теряет по одной единице воды в минуту, независимо от того, находится оно
на радиаторе или нет. Если же вещь кладут на радиатор, то она теряет
дополнительно ещё k – 1 единиц воды в минуту, то
есть всего k единиц в минуту.
Если для сушки всех вещей достаточно m минут, то каждую вещь с ai > m необходимо дополнительно
сушить на радиаторе. Объём воды, который не успеет испариться естественным
образом, составляет ai – m. За одну минуту радиатор удаляет
дополнительно (k – 1) единиц воды, поэтому на такую вещь потребуется
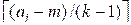
минут радиаторного
времени.
Суммарное количество минут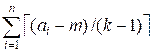 
использования радиатора не
должно превышать m, так как в каждую минуту можно сушить только одну
вещь. Суммирование берется по всем индексам i, для которых ai > m.
Таким образом, проверка
осуществляется следующим образом: если для заданного m общее количество
необходимых минут сушки на радиаторе не превышает m, то значение m
допустимо. Наименьшее подходящее значение m ищем с помощью бинарного
поиска.
Пример
Изначально
имеются три вещи с количеством воды (2, 3, 9).
В первую минуту кладём третью вещь на
радиатор. После этого получаем: (1, 2, 4).
Во вторую минуту снова
кладём третью вещь на радиатор. Состояние становится (0, 1, 0).
На третьей минуте вторая
вещь высыхает сама. Окончательное состояние: (0, 0, 0).
Рассмотрим
значение m = 2. Тогда все вещи, содержащие не более 2 единиц воды,
высохнут сами.
Для остальных
потребуется сушка на радиаторе. Вторая вещь содержит 3 единицы воды,
следовательно, на радиаторе необходимо удалить 3 – 2 = 1 единицу.
Третья вещь
содержит 9 единиц, поэтому на радиаторе нужно удалить 9 – 2 = 7 единиц воды.
На это
потребуется 
+ 
= 3 минуты. Это больше чем m = 2. Следовательно, двух минут
недостаточно.
Реализация алгоритма
Объявим рабочий
массив.
#define MAX 100001
int a[MAX];
Читаем входные данные.
scanf("%d",&n);
for(i = 0; i < n; i++) scanf("%d",&a[i]);
scanf("%d",&k);
За r минут все
белье обязательно высохнет, даже без использования радиатора.
l = 0; r =
*max_element(a,a+n);
Если k ≤ 1,
то сушка с использованием радиатора эквивалентна естественной сушке, и радиатор не
даёт никакого преимущества.
if (k <= 1)
{
printf("%d\n",r);
return 0;
}
Искомое минимальное количество минут m можно найти
бинарным поиском на отрезке [l; r].
while
(r - l > 1)
{
m = (r + l) / 2;
Переменная dry
накапливает общее количество минут, в течение которых необходимо использовать
радиатор. При этом за m минут следует высушить всё бельё.
dry = 0;
for (i = 0; i < n; i++)
{
if (a[i]
> m)
dry += (a[i] - m + k - 2) / (k - 1);
if (dry
> m) break;
}
if (dry >
m) l = m; else r = m;
}
Выводим ответ.
printf("%d\n",r);