5471. Граф 1, 1/2,
1/3, 1/4
Дан связный, взвешенный
неориентированный граф, ребра которого имеют веса 1, 1/2, 1/3, 1/4.
Найдите кратчайший путь от вершины 1 до всех остальных.
Вход. В первой строке записаны два
натуральных числа n и m (1 ≤ n ≤ 5 * 105,
1 ≤ m ≤ 8 * 105) – количество вершин и ребер графа соответственно. Далее записаны ребра на отдельных
строках. Ребра задаются тремя натуральными числами: u, v и w (1 ≤ u, v ≤ n, u ≤ v, 1 ≤ w ≤ 4), которые обозначают наличие
ребра из u в v веса 1 / w.
Выход. Для каждой вершины от 2 до n
выведите одно число – длину кратчайшего пути от вершины 1 до
нее, с точностью не менее 8 знаков после запятой.
|
Пример
входа |
Пример
выхода |
|
4 4 1 2 1 2 3 2 3 4 4 4 1 3 |
1.00000000 0.58333333 0.33333333 |
РЕШЕНИЕ
поиск в
ширину
Анализ алгоритма
Сделаем веса
ребер целочисленными. Для этого поделим 12 на w (то же самое что вес ребра умножить на
12). Например, вершины 2 и 3 соединяет ребро весом 1/2 (w = 2). Имеем: 12
/ w = 12 / 2 = 6. Или
1/2 * 12 = 6, что есть то же самое.
Имеем граф с целочисленными
ребрами 3, 4, 6, 12. Для нахождения кратчайших расстояний запустим 1-k поиск в ширину
для k = 12.
1-k поиск в ширину известен
как алгоритм Дайала – модификация Дейкстры для малых целочисленных весов ребер.
https://www.geeksforgeeks.org/dials-algorithm-optimized-dijkstra-for-small-range-weights/
Пример
Рассмотрим
граф из примера. Домножим веса всех ребер на 12 чтобы они стали целочисленными.
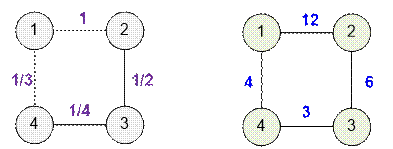
Реализация алгоритма
Константа MAX равна наибольшему
возможному числу вершин в графе. Объявим массивы кратчайших расстояний dist и пройденных
вершин used.
#define MAX 500010
int dist[MAX], used[MAX];
Граф храним в списке смежности g. g[i] содержит
информацию о смежных вершинах в виде пар. Пара чисел содержит вершину, куда
направлено ребро и его вес.
vector<vector<pair<int, int>>> g; // (to, dist)
Для реализации 1-k BFS объявим как минимум k = 13 очередей (очереди
нумеруются от 0 до 12).
queue<int> q[14];
Функция bfs реализует 1-k поиск в ширину из вершины start.
void bfs(int start, int k)
{
Переменная pos содержит номер текущей обрабатываемой очереди.
int pos = 0; //
current queue
Инициализируем массив кратчайших расстояний dist.
memset(dist, 0x3F, sizeof(dist));
dist[start] = 0;
Заносим начальную вершину в очередь 0. Кратчайшее расстояние
от start до start равно 0.
q[0].push(start);
Переменная cnt хранит общее количество вершин, находящихся в очередях.
int cnt = 1; // number
of vertices in the queues
Основной цикл поиска в ширину. Продолжаем его пока хотя бы
одна очередь содержит хотя бы одну вершину.
while (cnt > 0)
{
Ищем непуствую очередь pos.
while (q[pos % (k + 1)].empty()) pos++;
Извлекаем вершину from из головы очереди pos.
int from = q[pos % (k + 1)].front();
q[pos % (k + 1)].pop();
Одна вершина из очереди удалена, уменьшаем cnt на 1.
cnt--; // one vertex popped
Если кратчайшее расстояние до вершины from уже посчитано (вершина
была обработана в других очередях), то пропускаем ее.
if (used[from]) continue; // from can be processed earlier
used[from] = 1;
Перебираем вершины, смежные с from.
for (int i = 0; i < g[from].size(); i++)
{
Обрабатываем ребро (from, to) весом d.
int to = g[from][i].first; // to
int d = g[from][i].second; // dist;
Если ребро релаксирует, то заносим в очередь номер dist[from] + d вершину to. Пересчитываем значение dist[to]. Новая вершина добавлена в очередь,
увеличим cnt на 1.
if (dist[to] > dist[from] + d)
{
q[(dist[from] + d) % (k + 1)].push(to);
dist[to] = dist[from] + d;
cnt++;
}
}
}
}
Основная часть программы. Читаем входные данные. Строим граф.
Пересчитываем веса ребер, делая их целочисленными.
scanf("%d %d", &n, &m);
g.resize(n + 1);
while (m--)
{
scanf("%d %d %d", &from,
&to, &d);
g[from].push_back(make_pair(to, 12 / d));
g[to].push_back(make_pair(from, 12 / d));
}
Запускаем 1-k поиск в ширину с k = 12.
bfs(1, 12);
Выводим ответ – кратчайшие расстояния от первой вершины до
всех остальных.
for (i = 2; i <= n; i++)
printf("%.8lf\n", dist[i] /
12.0);
Реализация алгоритма – Дейкстра
Рассмотрим решение
задачи алгоритмом Дейкстры.
#include <cstdio>
#include <vector>
#include <cstring>
#include <queue>
#define MAX 500010
using namespace std;
int i, j, n, m, a, b, from, temp;
int d[MAX];
struct Vertex
{
int to, dist;
} v;
vector<vector<Vertex> > g;
queue<int> q;
void Dijkstra(int start)
{
memset(d, 0x3F, sizeof(d));
d[start] = 0;
q.push(start);
while (!q.empty())
{
int v = q.front();
q.pop();
for (int i = 0; i < g[v].size(); i++)
{
int to = g[v][i].to;
int dist = g[v][i].dist;
if (d[to] > d[v] + dist)
{
d[to] = d[v] + dist;
q.push(to);
}
}
}
}
int main(void)
{
scanf("%d %d", &n,
&m);
g.resize(n + 1);
while (m--)
{
scanf("%d %d %d", &from,
&v.to, &v.dist);
v.dist = 12 / v.dist;
g[from].push_back(v);
swap(from, v.to);
g[from].push_back(v);
}
Dijkstra(1);
for (i = 2; i <= n; i++)
printf("%.8lf\n", d[i] / 12.0);
return 0;
}