5472. RMQ
Задан массив из n целых чисел и m запросов вида: найти минимум на отрезке с концами li, ri.
Вход. Состоит из t
тестов. Каждый тест задаётся числами n,
m, a, b (1 ≤ n ≤ 25000, 1 ≤ a, b
≤ 109), где n –
размер массива, m – число запросов.
Массив и запросы нужно получить следующим образом: выпишем последовательность
чисел a·1 + b, a·2 + b, ..., a·(n + 2·m) + b,
взятых по модулю 232. Первые n
чисел последовательности – элементы массива, числа с n + 1 по n + 2·m, взятые по модулю n, образуют m пар чисел li – 1, ri – 1 - запросы.
Ввод заканчивается строкой 0 0 0 0.
Сумма n по всем
наборам тестов не превосходит 109, cумма m по всем наборам тестовых данных не превосходит 20000000.
Выход. Для каждого
теста выведите в отдельной строке сумму по всем запросам.
|
Пример
входа |
Пример
выхода |
|
10 10
955379886 619166003 0 0 0 0 |
7671393960 |
Пояснение
Сначала рассмотрим процесс
генерации последовательности из n = 10 элементов. У нас a = 955379886, b
= 619166003. Последовательность имеет вид
a·1 + b, a·2 + b, ..., a·10 + b,
где каждый
элемент взят по модулю 232. Например,
a1 = (a·1 + b) mod 232 = (955379886 * 1 + 619166003) mod 232 = 1574545889,
a2 = (a·2 + b) mod 232 = (955379886 * 2 + 619166003) mod 232 = 2529925775,
…
a10 = (a·10 + b) mod 232 = (955379886 * 10 + 619166003) mod 232 =
10172964863 mod 4294967296 = 1583030271

Следующие числа a·11
+ b, a·12 + b, … , взятые по
модулю 232, а затем по модулю n
= 10, образуют m пар запросов (li – 1, ri – 1). Первый запрос:
(a·11 + b) mod 232 mod 10 = (955379886 * 11 + 619166003) mod 232 mod 10 =
2538410157 mod 10 = 7
(a·12 + b) mod 232 mod 10 = (955379886 * 12 + 619166003) mod 232 mod 10 =
3493790043 mod 10 = 3
Итак, (l1 – 1, r1 – 1) = (7, 3), следовательно (l1, r1)
= (8, 4).
Запросы:
8 4 -> 145718251
4 10 -> 145718251
6 2 -> 145718251
8 8 -> 3967237795
4 10
6 6
2 8
4 10
10 6
2 8
РЕШЕНИЕ
структуры
данных - RMQ
Анализ алгоритма
Решение с
препроцессингом O(nlog2n) по времени даст Time Limit. Реализуем
препроцессинг за O(n) с выполнением
запроса за O(log2n).
Пусть a1, a2, …, an
– входная последовательность. Построим массив mas[log2n][n],
ячейка mas[i][j] (0 ≤ i ≤
log2n, 0 ≤ j ≤ n – 1) которого содержит min(a2^i*j,
…, a2^i*(j+1)-1).
Вычисления можно провести при помощи следующей рекуррентности:
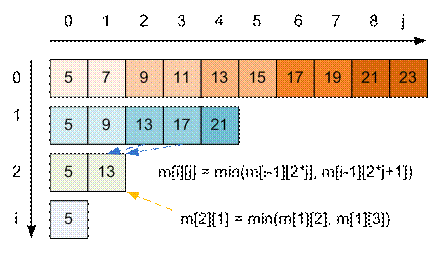
mas[i][j] = min (mas[i – 1][2j], mas[i – 1][2j + 1] ,
mas[0][i] = ai
Пример
Четверка входных
данных 10 5 2 3 сгенериует следующий массив.
Реализация алгоритма
Поскольку
элементы входной последовательности берутся по модулю 232, будем
проводить все вычисления с беззнаковым целочисленным типом unsigned int.
#define MAX 25010
#define LOGMAX 15
#define INF 4294967295u
unsigned int
mas[LOGMAX][MAX];
Нахождение
минимума на интервале (al,
…, ar-1).
unsigned int
RMQ(int l, int
r)
{
unsigned int res = INF;
int d = 0;
while (l !=
r)
{
if (l &
1)
{
if
(mas[d][l] < res) res = mas[d][l];
l++;
}
if (r &
1)
{
r--;
if
(mas[d][r] < res) res = mas[d][r];
}
l >>= 1; r >>= 1; d++;
}
return res;
}
Основная часть
программы. Читаем входные данные. Генерируем последовательность ai и заносим его в массив
mas[0].
while(scanf("%u
%u %u %u",&n,&m,&a,&b), n + m + a + b)
{
mas[0][0] = a + b;
for(i = 1; i
< n; i++)
mas[0][i] = mas[0][i-1] + a;
Препроцессинг – заполнение массива
mas за O(n).
r = n;
for(i = 1; r
> 1; i++)
{
for(j = 0;
j < r / 2; j++)
{
mas[i][j] = mas[i-1][2*j];
if
(mas[i][j] > mas[i-1][2*j+1]) mas[i][j] = mas[i-1][2*j+1];
}
r /= 2;
}
Генерируем запросы и вычисляем их
результаты.
cur = mas[0][n-1];
for(res = 0,
i = 1; i <= 2 * m; i += 2)
{
cur += a; l = cur % n;
cur += a; r = cur % n;
if (l >
r) temp = l, l = r, r = temp;
res += RMQ(l,r+1);
}
Выводим ответ на очередной тест.
printf("%lld\n",res);
}