5491. Муу

Коровы подсели на новую игру в слова, называемую "Муу". В нее играют несколько коров, стоящих в линию. Каждая корова должна назвать одну определенную букву как можно быстрее. Корова, которая ошибется, выбывает из игры.

Последовательность букв в игре Муу бесконечна. Начинается она так:

m o o m o o o m o o m o o o o m o o m o o o m o o m o o o o o

Наилучшим образом последовательность задается рекурсивно: пусть S(0) – слово из 3-х букв "m o o". Последовательность S(k) получается из копии последовательности S(k – 1), слова "m o ... o" с k + 2 буквами o, за которым следует еще одна копия последовательности S(k – 1). Например:

S(0) = "m o o"

S(1) = "m o o m o o o m o o"

S(2) = "m o o m o o o m o o m o o o o m o o m o o o m o o"

Можно заметить, что таким образом строится бесконечно длинная строка, и именно она используется в игре Муу. Бесси, мудрая корова, хочет узнать n – ую букву этой последовательности: какой она будет – "m" или "o"? Помогите ей узнать это!

Вход. Одно целое число n (1 ≤ n ≤ 10⁹).

Выход. Одна буква – m или o.

Пример входа	Пример выхода
11	m

РЕШЕНИЕ

рекурсия

Анализ алгоритма

Ищем наименьшее k, для которого S(k) содержит n-ую букву. Далее определяем, в какой из трех частей S(k) лежит n-ая буква. Она лежит либо во второй части (посередине), либо в третьей (в этом случае положим m равным сумме длин первой и второй частей и запустим поиск (n – m)-ой буквы в S(k – 1), так как третья часть S(k) полностью совпадает с S(k – 1)).

Пример

Пусть необходимо определить n = 20 -ую букву. Поскольку длина S(2) равна 10, а длина S(3) равна 25, то 20-ая буква лежит в S(3).

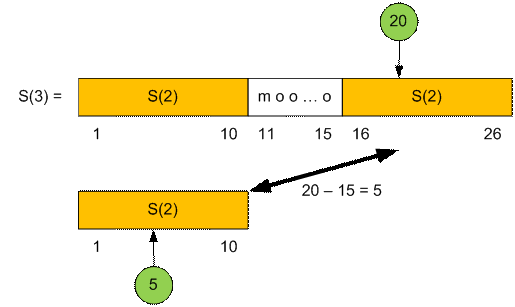
20-ая буква лежит в третьей части S(3), равной S(2). Следовательно 20-ая буква будет такой же, как и 20 – 15 = 5-ая буква S(2).

Реализация алгоритма

Функция len(k) возвращает длину последовательности S(k).

int len(int k)

{

if (k == -1) return 0;

int x = len(k - 1);

return x + k + 3 + x;

}

Поиск n-ой буквы в последовательности S(k).

char Solve(int n, int k)

{

Если длина S(k) меньше чем n, то следует искать n-ую букву в S(k + 1).

if (n > len(k)) return Solve(n,k+1);

Если n не больше длины S(k – 1), то следует искать n-ую букву в S(k – 1).

if (n <= len(k-1)) return Solve(n,k-1);

Поскольку n > len(k – 1), то n-ую букву следует искать или посередине, или во второй части S(k).

n = n - len(k-1);

Проверим, лежит ли n-ая буква в средней части последовательности S(k).

if (n <= k + 3)

return (n == 1) ? 'm' : 'o';

n-ая буква находится в последней части S(k). Это все равно что искать ее в последовательности S(k – 1).

n = n - (k + 3);

return Solve(n,k-1);

}

Основная часть программы. Начинаем искать n-ую букву в S(0).

scanf("%d",&n);

printf("%c\n",Solve(n,0));

Java реализация

import java.util.*;

public class Main

{

static int len(int k)

{

if (k == -1) return 0;

int x = len(k - 1);

return x + k + 3 + x;

}

static char Solve(int n, int k)

{

if (n > len(k)) return Solve(n,k+1);

if (n <= len(k-1)) return Solve(n,k-1);

n = n - len(k-1); /* Discount S(k-1) from beginning of string */

if (n <= k+3) /* n in middle section? */

return (n == 1) ? 'm' : 'o';

n = n - (k+3);

return Solve(n,k-1);

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

System.out.println(Solve(n,0));

con.close();

}

}