5542. AB-поэмы
Современная
рекурсивная AB-поэма создается из заданного стиха W и двух фраз Pa и Pb, все они являются словами в алфавите {a, b}.
Первый стих поэмы W1 = W, а n-ый
стих получается из (n – 1)-го заменой
каждой a в Wn-1
фразой Pa, и каждой b фразой Pb.
Вы
организовываете ежегодное чтение AB-поэмы, по одному стиху каждый год. Оцените,
как будет меняться время чтения стихов в будущем. Другими словами, найдите
границу:
![]()
где |Wn| обозначает общее
количество букв в n-ом стихе поэмы.
Вход. Первая строка содержит количество тестов t. Каждый тест состоит из трех строк,
каждая из которых содержит слово в алфавите {a, b}. Этими словами
являются соответственно Pa,
Pb и W. Слова не пустые и
содержат не более 1000 символов.
Выход. Для каждого
теста в отдельной строке вывести одно действительное число: границу,
вычисленную программой. Разрешена ошибка вычислений порядка 10-9.
Если граница не существует, вывести один знак минус (-).
|
Пример
входа |
Пример
выхода |
|
2 ab a ab bb aaa baa |
1.61803398875 - |
РЕШЕНИЕ
собственные
числа и вектора
Анализ алгоритма
Составим вектор
(aa, ab), где aa равно
количеству букв ‘а’ во фразе Pa, а ab равно
количеству букв ‘b’ во фразе Pa. Аналогично составим вектор (ba, bb), где ba равно
количеству букв ‘а’ во фразе Pb, а bb равно количеству букв ‘b’ во фразе Pb. Пусть стих Wi содержит wa букв ‘а’ и wb букв ‘b’. Поскольку нас интересуют только длины Wi, то порядок следования букв во фразах и стихах для нас
несущественен. Обозначим
количество букв ‘а’ и ‘b’
в стихе Wi+1 равными na и nb.
Составим матрицу
A = 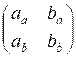 . Тогда
. Тогда
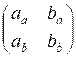 *
* ![]() =
= 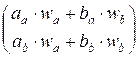 =
= ![]()
Пусть v1 и v2 – собственные вектора матрицы А. Тогда существуют такие собственные
чяисла λ1 и λ2, что Av1
= λ1v1 и Av2 = λ2v2. Разложим
вектор x = (xa,
xb) по базису v1 и v2.
Здесь xa равно
количеству букв ‘а’ в W, а xb равно
количеству букв ‘b’ в W. Пусть
x = c1
* v1 + c2 * v2, где здесь c1 и c2 – некоторые константы
Количество букв
в стихе Wn равно сумме
координат в векторе An-1 * x. Учитывая что из Av = λv следует Anv = λnv, Имеем:
An * x = An * (c1 * v1 + c2 * v2) = c1 * An * v1 + c2 * An * v2 =
c1 * λ1n
* v1 + c2 * λ2 n * v2
Пусть v1 = (v11, v12), v2 = (v21, v22). Тогда
An * x = c1 * λ1n * ![]() + c2 * λ2 n *
+ c2 * λ2 n * ![]() =
= 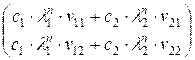
Тогда |Wn| = ![]() .
.
Следовательно
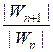 =
= 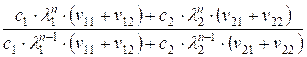 =
= 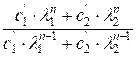
Если c1 = 0 (тогда и c1' = c1 * (v11 + v12)
=
0), то искомая граница равна λ2.
Если c2 = 0 (тогда и c2' = c2 * (v21 + v22) = 0), то искомая
граница равна λ1.
Пусть λ1 > λ2. Разделим
числитель и знаменатель дроби на ![]() :
:
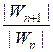 =
= 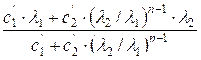
Или
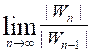 =
= 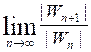 =
= ![]() = λ1
= λ1
Если λ2 = -λ1, то
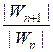 =
= 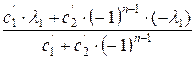 =
= 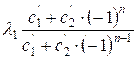
Вычислим собственные значения матрицы A
= 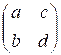 . Решаем уравнение |A – λE| = 0, или
. Решаем уравнение |A – λE| = 0, или 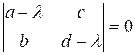 . Имеем: (a
– λ) * (d – λ) – bc = 0, λ2 – λ (a + d)
+ ad – bc = 0. Дискриминант disc квадратного уравнения равен (a + d)2
– 4(ad – bc) = (a – d)2 + 4bc.
. Имеем: (a
– λ) * (d – λ) – bc = 0, λ2 – λ (a + d)
+ ad – bc = 0. Дискриминант disc квадратного уравнения равен (a + d)2
– 4(ad – bc) = (a – d)2 + 4bc.
Собственные значения равны 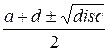 . Для того чтобы λ2 = -λ1 необходимо a + d = 0. Но поскольку a и d неотрицательны (это количество букв в соответствующих строках), то a + d = 0 возможно лишь
при a = d = 0. В этом случае λ1,2 =
. Для того чтобы λ2 = -λ1 необходимо a + d = 0. Но поскольку a и d неотрицательны (это количество букв в соответствующих строках), то a + d = 0 возможно лишь
при a = d = 0. В этом случае λ1,2 =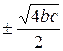 =
= ![]() .
.
Рассмотрим
случай b = c, матрица A имеет вид 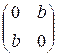 . Тогда
. Тогда
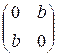
![]() =
= ![]() ,
, 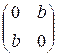
![]() =
= 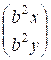
Сумма координат |An * x| = bn(x + y), следовательно 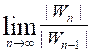 = b.
= b.
Однако при a = d = 0 и b ≠ c
искомой границы не существует.
Пример
Пусть Pa = ab, Pb = a. Тогда матрица А примет
вид: A = 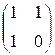 . Рассмотрим процесс преобразования стихов поэмы:
. Рассмотрим процесс преобразования стихов поэмы:
W1 =
W = ab, W2 = aba, W3 = abaab, W4 =
abaababa, W5 = abaababa, …
Или в матричном
виде:
W2: 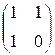
![]() =
= ![]() , W3:
, W3: 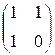
![]() =
= ![]() ,
,
W4: 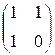
![]() =
= ![]() , W5:
, W5: 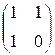
![]() =
= ![]()
Реализация алгоритма
#define MAX 1010
char Pa[MAX], Pb[MAX], w[MAX];
Используется при обработке входных
данных. Подсчитываем количество букв 'a' и ‘b’ в строке s соответственно в
переменных a и b.
void CountAB(char
*s, int &a, int
&b)
{
for(int i = a = b = 0; i < strlen(s); i++)
if (s[i] ==
'a') a++; else
b++;
}
Основная часть программы. Для каждого
теста читаем входные данные. В каждой входной строке подсчитываем количество
букв ‘a’ и ‘b’.
scanf("%d\n",&t);
while(t--)
{
gets(Pa); CountAB(Pa,a,b);
gets(Pb); CountAB(Pb,c,d);
gets(w);
CountAB(w,x,y);
Вычислим 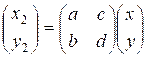 .
.
x2 = a * x + c * y;
y2 = b * x + d * y;
Если вектора (x, y) и (x2, y2) коллинеарны (тогда x / x2 = y / y2 или y * x2 = x * y2), то вектор (x, y) является собственным, и ответ
равен x2 / x или y2 / y (в зависимости от того, равно ли x нулю).
if (y * x2
== x * y2)
res = (x) ? 1.0 * x2 / x : 1.0 * y2 / y;
else
Если a = d
= 0, а b = c,
то большее
собственное значение матрицы 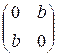 равно b.
равно b.
if (!a
&& !d) {
if (b
== c) res = b;
else
{
printf("-\n");
continue;
}
}
else
{
Находим собственные значения матрицы A
= 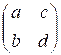 , решая
уравнение |A - λE| = 0. Вычисляем дискриминант disc квадратного уравнения.
, решая
уравнение |A - λE| = 0. Вычисляем дискриминант disc квадратного уравнения.
disc = (a - d) * (a - d) + 4 * b * c;
Больший корень (собственное значение)
равен 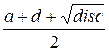
res = (a + d + sqrt(disc)) / 2.0;
}
Выводим найденный ответ.
printf("%.12lf\n",res);
}