5621. Найти кратное

 

Имеется n натуральных чисел, каждое из которых не больше 15000. Они не обязательно различны (два или более числа могут быть одинаковыми). Необходимо выбрать некоторое количество few (1 ≤ few ≤ n) этих чисел так, чтобы их сумма делилась на n (то есть n * k = (сумме выбранных чисел) для некоторого числа k).

 

Вход. Первая строка содержит число n (n ≤ 10000). Каждая из следующих n строк содержит одно из имеющихся чисел.

 

Выход. Если требуемое множество чисел не найдено, то вывести 0. Иначе в первой строке вывести количество выбранных чисел, а затем и сами числа (по одному в отдельной строке) в произвольном порядке. Если существует более чем одно множество чисел с требуемыми свойствами, то вывести любое из них.

 

Пример входа

Пример выхода

5

1

2

3

4

1

2

2

3

 

 

РЕШЕНИЕ

математика

 

Анализ алгоритма

Пусть d1, d2, …, dn – входные числа. Рассмотрим все частичные суммы si = d1 + … + di. Поскольку частичных сумм имеется в точности n, то среди всех значений si mod n обязательно найдутся либо два одинаковых, либо такое i что si mod n = 0.

Если sa-1 mod n = sb mod n для a – 1 < b, то da + … + db делится на n. Набор чисел da, da + 1, …, db будет искомым. Если существует такое i, что si mod n = 0, то искомыми будут числа d1, d2, …, di.

 

Пример

Рассмотрим приведенный пример. Вычислим все частичные суммы:

 

 

 

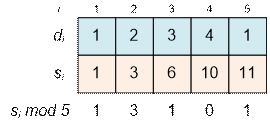
Искомых наборов имеется несколько. Например:

·        поскольку s1 = s3, то d2 + d3 = 5 делится на 5.

·        поскольку s1 = s5, то d2 + d3 + d4 + d5 = 10 делится на 5.

·        поскольку s3 = s5, то d4 + d5 = 5 делится на 5.

·        поскольку s4 = 0, то d1 + d2 + d3 + d4 = 10 делится на 5.

 

Реализация алгоритма

Входные числа будем хранить в массиве d. Массив r будем использовать для отмечания частичных сумм: если s = d1 + … + di, то положим r[s] = i.

 

#define MAX 10100

int d[MAX], r[MAX];

 

Набором чисел, сумма которых делится на n, будут d[a], d[a + 1], …, d[b]. Выводим их количество b – a + 1, а также сами числа по одному в одной строке.

 

void print(int a, int b)

{

  printf("%d\n",b - a + 1);

  for(int i = a; i <= b; i++)

    printf("%d\n",d[i]);

}

 

Основная часть программы.

 

memset(r,-1,sizeof(r)); r[0] = 0;

scanf("%d",&n);

for(sum = 0, i = 1; i <= n; i++)

{

  scanf("%d",&d[i]);

  sum = (sum + d[i]) % n;

 

Если вторично встретилась частичная сумма, равная sum, то выводим набор требуемых чисел dr[sum] + 1, …, di.

 

  if (r[sum] != -1)

  {

    print(r[sum]+1,i);

    break;

  }

  else r[sum] = i;

}