5668. Сделка с нефтью
Нефть – очень важный
стратегический ресурс. Недавно Соединенные Штаты Антарктики вторглись в очень
богатую нефтью страну Кари, и теперь стараются держать контроль над ее
нефтетранспортной системой. Система состоит из трубопроводов, соединяющих
различные узлы – источники нефти и главные города и порты стран. Он
сконструирован таким образом, что можно транспортировать нефть из любого узла в
любой другой.
Однако противостоящие
национальные силы Кари не удовлетворены ситуацией. Они постоянно совершают
теракты, взрывая некоторые нефтепроводы. Недавно террористы решили выполнить
серию взрывов и хотят причинить системе нефтепроводов как можно больший ущерб.
Для каждого трубопровода
террористы знают стоимость взорвать его. Они имеют фиксированную сумму денег и
хотят взорвать как можно больше труб на эту сумму. Однако, поскольку им
по-прежнему нужна нефть для себя в разных регионах страны, они хотят чтобы
система по-прежнему была в состоянии транспортировать нефть из любого узла до
любого другого. Помогите им установить, какие трубы следует взорвать.
Вход.
Первая строка содержит количество вершин n,
количество трубопроводов m и
количество денег s у террористов (2 ≤
n ≤ 50000, 1 ≤ m ≤ 105, 0 ≤ s ≤ 1018). Следующие m строк содержат информацию о трубопроводах
– номера вершин, соединяемые трубопроводом, и стоимость его подрыва (она не
превосходит 109).
Нефть можно передавать вдоль
каждого трубопровода в обоих направлениях, каждые два узла соединены не более
чем одним трубопроводом.
Выход.
Выведите в первой строке максимальное количество трубопроводов, которое смогут
взорвать террористы. Во второй строке выведите номера этих трубопроводов (они
пронумерованы начиная с 1 в порядке их появления во входных данных).
|
Пример входа |
Пример выхода |
|
6 7 10 1 2 3 1 3 3 2 3 3 3 4 1 4 5 5 5 6 4 4 6 5 |
2 1 5 |
РЕШЕНИЕ
графы – система
непересекающихся множеств
Анализ алгоритма
Найдем
максимальное остовное дерево (остов с максимальным весом). Ребра, не входящие в
него, поместим в массив w. Любое подмножество
ребер из w может
быть удалено. Нам следует максимизировать количество удаленных ребер при
ограниченном количестве
денег s у террористов. Отсортируем
ребра в w по возрастанию веса и будем взрывать
трубопроводы по возрастанию их стоимости до тех пор, пока хватит денег (сумма стоимостей
взорванных трубопроводов не должна превышать s).
Пример
Граф из
примера имеет вид:
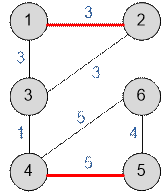
Террористы могут взорвать 2
трубопровода: (1, 2) и (4, 5) общей стоимостью 3 +
5 = 8, что не
больше 10.
Этот тест
имеет не единственное решение. Максимальный остов имеет вид:
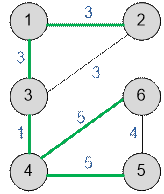
Массив w будет содержать ребра, не
входящие в максимальный остов: (2, 3), (5, 6). Суммарная стоимость этих ребер
не превосходит 10, поэтому взорвать их можно все.
Реализация алгоритма
Объявим
структуру ребра Edge. Она
содержит соединяющие вершины u и v, вес cost и номер Id ребра.
struct Edge
{
int u, v, cost, Id;
} temp;
Функция Repr возвращает представителя множества, в котором находится n.
int Repr(int n)
{
if (n == mas[n]) return n;
return mas[n] = Repr(mas[n]);
}
Функция Union объединяет множества с элементами x и y.
int Union(int x, int y)
{
int x1 = Repr(x), y1 = Repr(y);
mas[x1] = y1;
return (x1 != y1);
}
Функция – компаратор cmpGreater сортирует
ребра по убыванию веса.
int cmpGreater(Edge a, Edge b)
{
return a.cost > b.cost;
}
Функция – компаратор cmpLess сортирует ребра по возрастанию
веса.
int cmpLess(Edge a, Edge b)
{
return a.cost < b.cost;
}
Основная
часть программы. Читаем входные данные.
scanf("%d %d %lld", &n, &m, &s);
Инициализируем массив mas.
mas.resize(n + 1);
for (i = 1; i <= n; i++) mas[i] = i;
Читаем ребра графа, заносими их в массив e.
for (i = 0; i < m; i++)
{
scanf("%d %d %d", &temp.u,
&temp.v, &temp.cost);
temp.Id = i + 1;
e.push_back(temp);
}
Сортируем ребра по убыванию веса.
sort(e.begin(), e.end(),
cmpGreater);
Строим максимальный остов. Ребра, не вошедшие в него,
заносим в массив w.
for (i = 0; i < e.size(); i++)
{
if (Repr(e[i].u) == Repr(e[i].v))
w.push_back(e[i]);
else
Union(e[i].u, e[i].v);
}
Сортируем ребра в массиве w.
sort(w.begin(), w.end(),
cmpLess);
Удаляем ребра из массива w по возрастанию их стоимости
до тех пор, пока хватит денег. Номера удаляемых ребер заносим в массив EdgeId.
for (i = 0; i < w.size(); i++)
{
if ((s < 0) || (w[i].cost > s)) break;
EdgeId.push_back(w[i].Id);
s -= w[i].cost;
}
Выводим ответ: количество удаленных ребер и их номера.
if (EdgeId.empty()) printf("0\n");
else
{
printf("%d\n", EdgeId.size());
for (i = 0; i < EdgeId.size(); i++)
printf("%d ", EdgeId[i]);
printf("\n");
}