5668. Oil deal

Oil is a very important strategic resource. Recently United States of Antarctica invaded the rich in oil country of Qari, and now try to keep the control of the oil transportation system. The system consists of pipelines that connect different nodes – oil sources and main country cities and ports. It is designed in such a way that it is possible to transport oil from any node to any other one.

However, the resisting native forces of Qari are not satisfied with the situation. So they continuously perform terror acts, blowing up some oil pipelines. Recently terrorists have decided to perform a series of explosions and want to hurt the oil pipeline system as much as possible.

For each pipeline the terrorists know the cost of blowing it up. They have a fixed sum of money and want to explode as many pipes as possible for this sum. However, since they still need oil for themselves in different regions of the country, they want the system still to be able to transport oil from any node to any other one. Help them to find out which pipes to blow up.

Input. The first line contains the number of nodes n, the number of pipelines m, and the amount of money s terrorists have (2 ≤ n ≤ 50000, 1 ≤ m ≤ 100000, 0 ≤ s ≤ 10¹⁸). The following m lines contain information about pipelines – for each pipeline the nodes it connects and the cost of blowing it up is specified (cost does not exceed 10⁹).

Oil can be transported along each pipeline in both directions, each two nodes are connected by at most one pipeline.

Output. On the first line print the maximal number of pipelines terrorists can blow up. On the second line print the numbers of these pipelines (pipelines are numbered starting with 1 as they are listed in the input file).

Sample input	Sample output
6 7 10 1 2 3 1 3 3 2 3 3 3 4 1 4 5 5 5 6 4 4 6 5	2 1 5

SOLUTION

graphs – dsu

Algorithm analysis

Find the maximum spanning tree (spanning tree with the maximum weight). The edges that are not included in it will be placed in the array w. Any subset of edges from w can be removed. We should maximize the number of removed edges with a limited amount of money s from terrorists. Sort the edges in w in ascending order of weight and blow up the pipelines in order of increasing value until there is enough money (the sum of the costs of the blown up pipelines should not exceed s).

Example

Graph from the sample has the form:

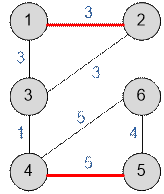
Terrorists can blow up 2 pipelines: (1, 2) and (4, 5) with a total cost of 3 + 5 = 8, which is no more than 10.

This test has more than one solution. The maximum spanning tree is:

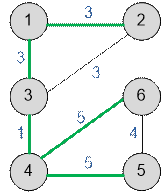
The array w will contain edges that are not in the maximum spanning tree: (2, 3), (5, 6). The total cost of these edges does not exceed 10, so all of them can be blown up.

Algorithm realization

Declare the edge structure Edge. It contains the connecting vertices u and v, the weight cost and the Id number of the edge.

struct Edge

{

int u, v, cost, Id;

} temp;

Function Repr finds a representative of the set that contains vertex n.

int Repr(int n)

{

if (n == mas[n]) return n;

return mas[n] = Repr(mas[n]);

}

Function Union unites sets that contain vertices x and y.

int Union(int x, int y)

{

int x1 = Repr(x), y1 = Repr(y);

mas[x1] = y1;

return (x1 != y1);

}

The function cmpGreater is a comparator that sorts the edges in descending order of weight.

int cmpGreater(Edge a, Edge b)

{

return a.cost > b.cost;

}

The function cmpLess is a comparator that sorts the edges in ascending order of weight.

int cmpLess(Edge a, Edge b)

{

return a.cost < b.cost;

}

The main part of the program. Read the input data.

scanf("%d %d %lld", &n, &m, &s);

Initialize the mas array.

mas.resize(n + 1);

for (i = 1; i <= n; i++) mas[i] = i;

Read the edges of the graph, store them into array e.

for (i = 0; i < m; i++)

{

scanf("%d %d %d", &temp.u, &temp.v, &temp.cost);

temp.Id = i + 1;

e.push_back(temp);

}

Sort the edges in descending order of weight.

sort(e.begin(), e.end(), cmpGreater);

Construct the maximum spanning tree. The edges that are not included in it are placed into the array w.

for (i = 0; i < e.size(); i++)

{

if (Repr(e[i].u) == Repr(e[i].v))

w.push_back(e[i]);

else

Union(e[i].u, e[i].v);

}

Sort the edges in the w array.

sort(w.begin(), w.end(), cmpLess);

Remove the edges from array w in ascending order of their weight until there is enough money. Push the numbers of the removed edges into the EdgeId array.

for (i = 0; i < w.size(); i++)

{

if ((s < 0) || (w[i].cost > s)) break;

EdgeId.push_back(w[i].Id);

s -= w[i].cost;

}

Print the answer: the number of removed edges and their numbers.

if (EdgeId.empty()) printf("0\n");

else

{

printf("%d\n", EdgeId.size());

for (i = 0; i < EdgeId.size(); i++)

printf("%d ", EdgeId[i]);

printf("\n");

}