5850. Математические платформы
В старых играх с двумерной
графикой можно столкнуться с подобной ситуацией. Какой-нибудь
герой прыгает по платформам (или островкам), которые висят в воздухе. Он
должен перебраться с одного края экрана до другого. Игрок может прыгнуть с
любой платформы i на любую
платформу k, затратив при этом (i – k)2 * (yi – yk)2 единиц
энергии, где yi и yk – высоты на которых
расположены эти платформы. Конечно же, энергию следует расходовать максимально
экономно.
Предположим, что вам известны
координаты всех платформ в порядке от левого края до правого. Сможете ли вы
найти, какое минимальное количество энергии потребуется герою, чтобы добраться
с первой платформы до последней?
Вход. В
первой строке записано количество платформ n (1 ≤ n ≤ 4000). Вторая строка
содержит n целых чисел, не превосходящих по
модулю 200000 – высоты, на которых располагаются платформы.
Выход. Выведите
единственное число – минимальное количество энергии, которое должен потратить
игрок на преодоление платформ.
|
Пример
входа |
Пример
выхода |
|
4 1 2 3 30 |
731 |
РЕШЕНИЕ
графы –
алгоритм Дейкстры
Анализ алгоритма
Рассмотрим
каждую платформу как вершину графа. Между каждой парой вершин i и j проведем неориентированное
ребро g[i][j]
весом
(i – j)2 * (yi – yj)2 (количество энергии, необходимое для перемещения
между вершинами i и j). Далее следует найти минимальный путь между первой и последней вершиной, что
можно совершить при помощи алгоритма Дейкстры.
Граф в памяти держать нет
необходимости, так как все значения g[i][j] при вычислениях пересчитываются по выше
указанной формуле.
Пример
Граф и его
весовая матрица имеют вид:
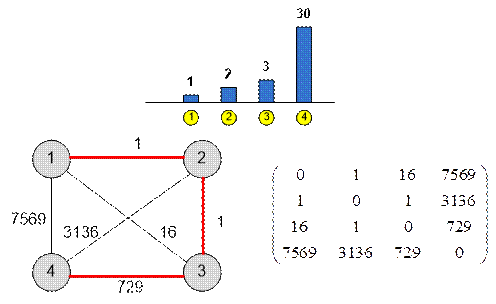
Герою следует
передвигаться по платформам в порядке 1 → 2 → 3 → 4, на что
следует потратить 1 + 1 + 729 = 731 единиц энергии.
Реализация алгоритма
Определим константы:
·
MAX – количество платформ;
·
INF – максимальное число типа kong long;
#define MAX 4001
#define INF
0x3F3F3F3F3F3F3F3FLL
Объявим рабочие массивы:
int used[MAX];
long long m[MAX], dist[MAX];
Читаем входные данные – высоты платформ. Платформы нумеруются
с 0 до n – 1.
scanf("%d", &n);
for (i = 0; i < n; i++)
scanf("%lld",
&m[i]);
Инициализируем массив кратчайших расстояний dist.
memset(dist, 0x3F, sizeof(dist));
dist[0] =
0;
Запускаем алгоритм Дейкстры из 0 вершины.
for (i = 1; i < n; i++)
{
min =
INF; w = -1;
for (j =
0; j < n; j++)
if
(!used[j] && dist[j] < min) { min = dist[j]; w = j; }
if (w
< 0) break;
for (j =
0; j < n; j++)
{
Вычисляем расстояние len между вершинами w и j.
long long len = (w - j)
* (w - j) * (m[j] - m[w]) * (m[j] - m[w]);
Если кратчайшее расстояние до вершины j еще не вычислено, то релаксируем ребро (w, j).
if
(!used[j] && dist[j] > dist[w]
+ len) dist[j] = dist[w] + len;
}
used[w]
= 1;
}
Выводим кратчайшее расстояние до вершины n – 1.
printf("%lld\n", dist[n - 1]);
Java реализация
printf("%lld\n", dist[n - 1]);
import java.util.*;
public class Main
{
static int used[];
static long m[], dist[];
static long INF = 1000000000000000000L;
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
m = new long[n];
for (int i = 0; i < n; i++)
m[i] = con.nextLong();
used = new int[n];
dist = new long[n];
Arrays.fill(dist, INF);
dist[0] = 0;
for (int i = 1; i < n; i++)
{
long min = INF;
int w = -1;
for (int j = 0; j < n; j++)
if (used[j] == 0 && dist[j] < min) { min = dist[j]; w = j; }
if (w < 0) break;
for (int j = 0; j < n; j++)
{
long len = (w - j) * (w - j) * (m[j] - m[w]) * (m[j] - m[w]);
if (used[j] == 0 && dist[j] > dist[w] + len)
dist[j] = dist[w] + len;
}
used[w] = 1;
}
System.out.println(dist[n-1]);
con.close();
}
}