5854. Maximum sum basic

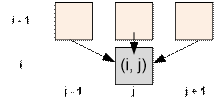
A rectangular table of size n rows by m columns is given. Each cell of this table contains one integer. You can traverse the table from top to bottom, starting from any cell in the top row, and at each step, move to one of the “lower neighboring” cells. In other words, from a cell with coordinates (i, j), you can move to (i + 1, j – 1), (i + 1, j), or (i + 1, j + 1). If j = m, the last of the three movement options is not possible. If j = 1, the first option is not possible. The route ends in one of the cells of the bottom row.

Write a program that finds the maximum possible sum of values of cells passed along any valid path.

Input. The first line contains n and m (1 ≤ n, m ≤ 200) – the number of rows and columns. Each of the next n lines contains m integers (with absolute values not exceeding 10⁶) – the values of the cells in the table.

Output. Print one single integer – the maximum possible sum.

Sample input	Sample output
4 3 1 15 2 9 7 5 9 2 4 6 9 -1	42

SOLUTION

dynamic programming

Algorithm analysis

Let a[i][j] be the input table. Let dp[i][j] represent the maximum sum of numbers along a path from any cell in the first row to the cell (i, j). Then

dp[i][j] = max(dp[i – 1][j – 1], dp[i – 1][j], dp[i – 1][j + 1]) + a[i][j]

To correctly calculate the values in the first and last columns, set

dp[i][0] = dp[i][m + 1] = -∞

Initialize the first row of the dp array with the values from the first row of the table а:

dp[1][i] = a[1][i], 1 ≤ i ≤ m

The answer to the problem will be the maximum value in the last (n-th) row of the dp array.

Example

Consider the input example.

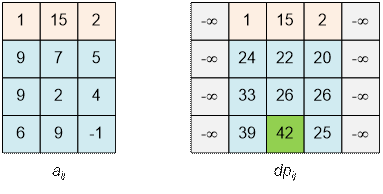
Algorithm implementation

Declare a constant MIN to store the minimum value, as well as arrays a and dp.

#define MAX 202

#define MIN -2000000000

int a[MAX][MAX], dp[MAX][MAX];

Read the input data. The top-left corner of the table will be stored in a[1][1]. Fill the columns with indices 0 and m + 1 in the dp array with the minimum possible value MIN.

scanf("%d %d", &n, &m);

for (i = 1; i <= n; i++)

{

dp[i][0] = dp[i][m + 1] = MIN;

for (j = 1; j <= m; j++)

scanf("%d", &a[i][j]);

}

Copy the first row of array a into the array dp.

for (i = 1; i <= n; i++)

dp[1][i] = a[1][i];

Recalculate the maximum sums along paths from the top row to the cell (i, j) and store them in the array dp.

for (i = 2; i <= n; i++)

for (j = 1; j <= m; j++)

dp[i][j] = max(max(dp[i - 1][j - 1], dp[i - 1][j]),

dp[i - 1][j + 1]) + a[i][j];

Find the largest number in the last (n-th) row of the dp array.

res = MIN;

for (i = 1; i <= m; i++)

if (dp[n][i] > res) res = dp[n][i];

Print the answer.

printf("%d\n", res);

Java implementation

import java.util.*;

public class Main

{

static int a[][], dp[][];

final static int MIN = -2000000000;

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int m = con.nextInt();

dp = new int[n+1][m+2];

a = new int[n+1][m+2];

for (int i = 1; i <= n; i++)

{

dp[i][0] = dp[i][m + 1] = MIN;

for (int j = 1; j <= m; j++)

a[i][j] = con.nextInt();;

}

for (int i = 1; i <= m; i++)

dp[1][i] = a[1][i];

for (int i = 2; i <= n; i++)

for (int j = 1; j <= m; j++)

dp[i][j] = Math.max(Math.max(dp[i - 1][j - 1], dp[i - 1][j]), dp[i - 1][j + 1]) + a[i][j];

int res = MIN;

for (int i = 1; i <= m; i++)

if (dp[n][i] > res) res = dp[n][i];

System.out.println(res);

con.close();

}

}