546. Быстрый побег
Братья Ньютон
планируют ограбить банк в городе Алвизо и хотят найти способ избежать всего
лишь одной полицейской машины города. Они знают, что их машина быстрее
полицейской. Поэтому если им удастся добраться до одной из магистралей, выходящих
из города, то они без особых проблем смогут оторваться от полиции.
Максимальная
скорость полицейской машины составляет
Братья хотят
найти такой маршрут, который будет им гарантировать возможность покинуть город,
независимо от того, какой маршрут выберет полицейская машина, и с какой
скоростью она будет передвигаться. Поскольку братья чувствуют себя не очень
уверенными водителями, то не хотят ехать быстрее, чем это необходимо. К
счастью, они недавно инвестировали в новую хай-тек систему отрыва от
полицейского автомобиля, которую Вы только что создали. Эта система сообщит Вам
минимально необходимую максимальную скорость, достаточную для избегания встречи
с полицейской машиной (а также и другие полезные вещи, как например, сам
маршрут).
Давайте немного
повернем время вспять, когда Вы были заняты построением системы эвакуации из
города и сосредоточены на поиске минимальной требуемой скорости. Можете ли Вы
найти ее правильно?
Все дороги можно
считать бесконечно узкими, а обе машины как точечные объекты. Если браться
окажутся в одной точке (на любой дороге или перекрестке) вместе с полицейской
машиной, то они будут пойманы. И по закону Мерфи произойдет то что должно
произойти. Обе машины начинают движение одновременно и могут ускориться /
замедлиться мгновенно в любой момент времени до любой скорости, не большей
максимально возможной. Они могут изменять дороги на перекрестках или
направление движения в любом месте дороги мгновенно независимо от текущей
скорости.
Вход. Первая строка содержит три целых числа n (2 ≤ n ≤ 100), m (1
≤ m ≤ 5000) и e (1 ≤ e ≤ n), где n – количество перекрестков, m – количество дорог в городе, e – количество существующих магистралей.
Далее следует m строк, каждая из которых содержит три целых числа a, b,
l (1 ≤ a < b ≤ n, 1 ≤ l ≤ 100), описывающих дорогу длины l (в сотнях метров) между перекрестками a и b. Далее следует
строка из e целых чисел, каждое из
промежутка 1...n, описывающих какой
из перекрестков соединен с существующей магистралью. Последняя строка содержит
два числа b и p (1 ≤ b, p ≤ n и b ≠ p), задающих перекрестки, с которых
соответственно стартуют братья и полицейская машина.
Всегда есть возможность добраться от одного перекрестка к
любому другому. Дороги соединяются только перекрестками (хотя могут
пересекаться в других местах используя мосты или тоннели). Дороги двусторонние,
между двумя перекрестками может быть не более одной дороги.
Выход. Вывести
наименьшую скорость в км/ч, достаточную для того чтобы убежать из города, или
слово IMPOSSIBLE, если это невозможно. В первом случае вывести ответ с
точностью 10-9.
|
Пример
входа |
Пример
выхода |
|
4 4 2 1 4 1 1 3 4 3 4 10 2 3 30 1 2 3 4 |
137.142857143 |
РЕШЕНИЕ
графы –
Дейкстра
Анализ
алгоритма
При помощи
алгоритма Дейкстры ищем кратчайшие расстояния до всех вершин для полиции.
Искомую скорость
братьев ищем бинарным поиском. Пусть она равна v0. Запускаем алгоритм Дейкстры поиска кратчайших путей
для братьев, причем движение в вершину возможно, если они там окажутся раньше
полиции. Если братья смогут добраться хотя бы до одной магистрали, то они
убегут от полиции, иначе нет. В зависимости от этого, используя бинарный поиск,
изменяем скорость братьев.
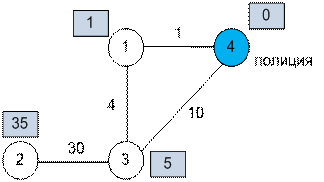
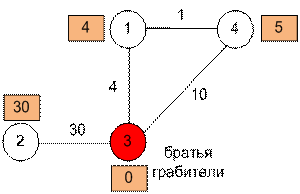
Пример
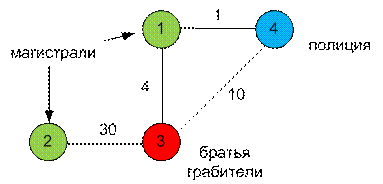
При помощи
алгоритма Дейкстры ищем кратчайшие расстояния до вершин для полиции (слева) и
для братьев (справа).
Реализация алгоритма
Объявляем
константы и глобальные переменные.
#define INF 0x3F3F3F3F
#define MAX 110
#define EPS 1e-9
int d[MAX][MAX], isHighWay[MAX];
int distPol[MAX], distBr[MAX],
used[MAX];
Релаксация ребра (v,
to) используя массив текущих
кратчайших путей dist.
void Relax(int
*dist, int v, int
to)
{
if (dist[to]
> dist[v] + d[v][to])
dist[to] = dist[v] + d[v][to];
}
Находим индекс минимального элемента в массиве dist среди еще
не просмотренных (для которых used[i]
= 0) вершин.
int Find_Min(int
*dist)
{
int i, v =
-1, min = 0x3F3F3F3F;
for(i = 1; i
<= n; i++)
if
(!used[i] && (dist[i] < min)) min = dist[i], v = i;
return v;
}
Алгоритм нахождения кратчайших путей из вершины source.
void Dijkstra(int
*dist, int source)
{
memset(used,0,sizeof(used));
dist[source] = 0;
for(int i = 1; i < n; i++)
{
int v =
Find_Min(dist);
for(int to = 1; to <= n; to++)
if
(!used[to]) Relax(dist,v,to);
used[v] = 1;
}
}
Основная часть программы. Читаем входные данные.
scanf("%d %d %d",&n,&m,&e);
memset(d,0x3F,sizeof(d));
memset(distPol,0x3F,sizeof(distPol));
memset(isHighWay,0,sizeof(isHighWay));
for(i = 0; i < m; i++)
{
scanf("%d %d
%d",&a,&b,&l);
d[a][b] = d[b][a] = l;
}
Если вершина i – магистраль, то установим isHighWay[i] = 1.
for(i = 0; i < e; i++)
{
int HW;
scanf("%d",&HW);
isHighWay[HW] = 1;
}
scanf("%d %d",&start,&police);
Вычисляем кратчайшие расстояния до
всех вершин для полиции.
Dijkstra(distPol,
police);
Ищем минимальную скорость vel братьев бинарным поиском на
промежутке [MinSpeed; MaxSpeed].
MinSpeed = 0;
MaxSpeed = INF;
while(MaxSpeed - MinSpeed > EPS)
{
vel = (MaxSpeed + MinSpeed) / 2;
memset(used,0,sizeof(used));
memset(distBr,0x3F,sizeof(distBr));
distBr[start] = 0;
Дейкстрой ищем минимальный путь до
вершин, до которых могут добраться братья.
int flag;
for(int i = 1; i < n; i++)
{
int v =
Find_Min(distBr);
if (v ==
-1) break;
for(int to = 1; to <= n; to++)
if
(!used[to] && (d[v][to] < INF))
{
Братья, двигаясь со скоростью vel, могут попасть в to только если они там окажутся раньше
полиции. Братья доберутся в to за
вермя (distBr[v] + d[v][to])
/ vel, а полиция за distPol[to] / 160.0.
if
((distBr[to] > distBr[v] + d[v][to]) &&
(distPol[to] / 160.0
> (1.0*distBr[v] + d[v][to]) / vel))
distBr[to] = distBr[v] + d[v][to];
}
used[v] = 1;
}
Проверяем, смогут ли братья добраться
хотя бы до одной магистрали. Если смогут, устанавливаем flag = 1.
flag = 0;
for(int i = 1; i <= n; i++)
if((distBr[i]
< INF) && isHighWay[i]) flag = 1;
В зависимости от значения flag продолжаем бинарный поиск.
if (flag)
MaxSpeed = vel; else MinSpeed = vel;
}
Выводим найденную скорость.
vel = (MaxSpeed
+ MinSpeed) / 2;
if (vel > INF - 1) printf("IMPOSSIBLE\n");
else printf ("%.9lf\n",
vel);