573. Полярные единички

Программист на Северном полюсе работал за компьютером в варежках и поэтому мог набирать только 0 и 1, а клавиша 0 запала. Сможет ли он набрать минимальное число, состоящее только из единиц и при этом кратное заданному числу n?

Вход. Одно число n (n ≤ 1000).

Выход. Выведите искомое число или “no”, если такого числа не существует.

Пример входа 1	Пример выхода 1
10	no
Пример входа 2	Пример выхода 2
57	111111111111111111

РЕШЕНИЕ

математика

Анализ алгоритма

Если n делится на 2 или на 5, то такого числа не существует.

Реализуем деление в столбик числа, состоящего только из единиц, на n. Положим x = 1. Будем приписывать к x единицу справа (x = 10 * x + 1) и вычислять остаток от деления результата на n. Повторяем эту процедуру пока в остатке не получится 0. Подсчитываем количество использованных единиц при делении. Из этого количества единиц и состоит искомое наименьшее число, которое делится на n.

Пример

Для n = 3 ответ равен 111.

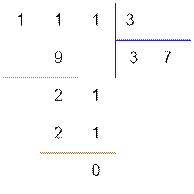
Реализация алгоритма

Читаем входное число n.

scanf("%d", &n);

Если n делится на 2 или на 5, то числа, состоящего только из единиц, не существует.

if ((n % 5 == 0) || (n % 2 == 0))

{

printf("no\n");

return 0;

}

Пусть x = 1. В переменной cnt подсчитываем количество использованных единиц.

x = cnt = 1;

Пока x не делится нацело на n, приписываем справа к x единицу и вычисляем остаток от деления x на n.

while (x > 0)

{

x = (10 * x + 1) % n;

cnt++;

}

Выводим ответ. Искомое число состоит из cnt единиц.

for (i = 0; i < cnt; i++)

printf("1");

printf("\n");

Python реализация

Читаем входное число n.

n = int(input())

Если n делится на 2 или на 5, то числа, состоящего только из единиц, не существует.

if n % 5 == 0 or n % 2 == 0:

print("no")

else:

Пусть x = 1. В переменной cnt подсчитываем количество использованных единиц.

x = cnt = 1

Пока x не делится нацело на n, приписываем справа к x единицу и вычисляем остаток от деления x на n.

while x > 0:

x = (10 * x + 1) % n

cnt += 1

Выводим ответ. Искомое число состоит из cnt единиц.

for i in range(cnt):

print("1", end="")

print()