5973. Выйти из строя!

n солдат построены в одну шеренгу. Сколькими способами можно выбрать из них несколько человек (хотя бы одного) так, чтобы среди вышедших не было стоящих рядом?

Вход. Одно число n (1 ≤ n ≤ 90).

Выход. Выведите искомое количество способов.

Пример входа	Пример выхода
3	4

РЕШЕНИЕ

рекуррентное соотношение

Анализ алгоритма

Обозначим через f(n) количество искомых способов. Отметим, что в f(n) входят только те способы, в которых ходя бы один солдат выходит из строя.

Очевидно, что f(1) = 1 (выходит один солдат) и f(2) = 2 (выходит или первый, или второй солдат).

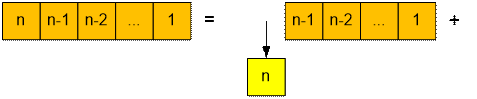
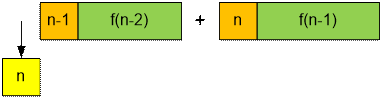
Пусть солдаты в строю пронумерованы в убывающем порядке от n до 1. Тогда выход из строя можно организовать одним из следующих трех способов:

· выходит n-ый, а все остаются на месте;

· выходит n-ый, тогда (n – 1)-ый должен остаться на месте. После чего рекурсивно рассматривается решение для (n – 2) солдат;

· n-ый остается на месте. Тогда рекурсивно решаем задачу для (n – 1) солдата;

Таким образом получили рекуррентное соотношение:

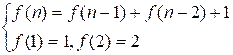
Пример

При n = 4 имеется 7 возможных способов.

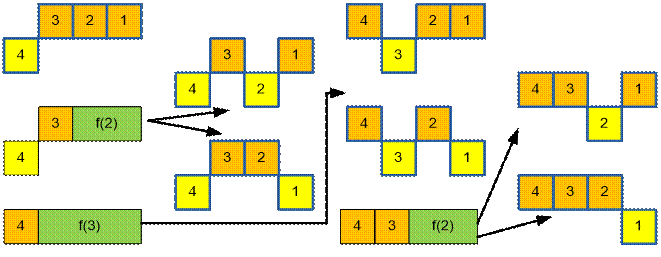
Реализация алгоритма

Значения функции f(i) будем запоминать в ячейках f[i].

#define MAX 91

long long res[MAX];

Вычислим значения f(i) (0 ≤ i ≤ MAX) по приведенной в анализе алгоритма формуле.

res[1] = 1; res[2] = 2;

for(i = 3; i < MAX; i++)

res[i] = res[i-1] + res[i-2] + 1;

Прочитаем входное значение n и выведем результат.

scanf("%d",&n);

printf("%lld\n", res[n]);

Реализация с запоминанием

#include <stdio.h>

#include <string.h>

#define MAX 91

long long m[MAX];

int i, n;

long long f(int n)

{

if (n == 1) return 1;

if (n == 2) return 2;

if (m[n] != -1) return m[n];

return m[n] = f(n-1) + f(n-2) + 1;

}

int main(void)

{

scanf("%d",&n);

memset(m,-1,sizeof(m));

printf("%lld\n",f(n));

return 0;

}

Java реализация

import java.util.*;

public class Main

{

public static void main(String[] args)

{

long res[] = new long[91];

res[1] = 1; res[2] = 2;

for(int i = 3; i < 91; i++)

res[i] = res[i-1] + res[i-2] + 1;

Scanner con = new Scanner(System.in);

int n = con.nextInt();

System.out.println(res[n]);

con.close();

}

}

Java реализация с запоминанием

import java.util.*;

public class Main

{

static int MAX = 91;

static long m[] = new long[MAX];

static long f(int n)

{

if (n == 1) return 1;

if (n == 2) return 2;

if (m[n] != -1) return m[n];

return m[n] = f(n-1) + f(n-2) + 1;

}

public static void main(String[] args)

{

Arrays.fill(m, -1);

Scanner con = new Scanner(System.in);

int n = con.nextInt();

System.out.println(f(n));

con.close();

}

}