5973. Out of the line!

n soldiers stay in one line. In how many ways can we choose some of them (at least one) so that among them there will not be soldiers standing in a line beside?

Input. One number n (1 ≤ n ≤ 90).

Output. Print one number – the answer to the problem.

Sample input	Sample output
3	4

SOLUTION

recurrent relation

Algorithm analysis

Let f(n) be the number of ways for soldiers to out of the line. Its obvious that f(1) = 1 and f(2) = 2.

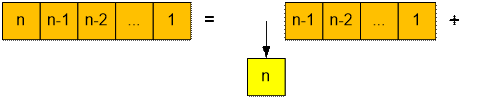
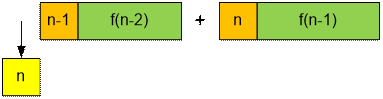
Let the soldiers in the row are numbered in decreasing order from n to 1. Then its possible to get out of the line with one of the next ways:

· n-th goes out, all others stay in a line;

· n-th goes out, then (n – 1)-st must stay in a line. Then recursively consider the solution for (n – 2) soldiers;

· n-th stay in a line. Then recursively solve the problem for (n – 1) soldiers;

So we get the recurrence relation:

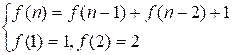
Algorithm realization

The value of function f(i) we shall store in f[i].

#define MAX 91

long long res[MAX];

Calculate the values f(i) (0 ≤ i ≤ MAX) according to formula given in analysis.

res[1] = 1; res[2] = 2;

for(i = 3; i < MAX; i++)

res[i] = res[i-1] + res[i-2] + 1;

Read input value n and print the answer.

scanf("%d",&n);

printf("%lld\n", res[n]);

Realization with memoization

#include <stdio.h>

#include <string.h>

#define MAX 91

long long m[MAX];

int i, n;

long long f(int n)

{

if (n == 1) return 1;

if (n == 2) return 2;

if (m[n] != -1) return m[n];

return m[n] = f(n-1) + f(n-2) + 1;

}

int main(void)

{

scanf("%d",&n);

memset(m,-1,sizeof(m));

printf("%lld\n",f(n));

return 0;

}

Java realization

import java.util.*;

public class Main

{

public static void main(String[] args)

{

long res[] = new long[91];

res[1] = 1; res[2] = 2;

for(int i = 3; i < 91; i++)

res[i] = res[i-1] + res[i-2] + 1;

Scanner con = new Scanner(System.in);

int n = con.nextInt();

System.out.println(res[n]);

con.close();

}

}

Java realization with memoization

import java.util.*;

public class Main

{

static int MAX = 91;

static long m[] = new long[MAX];

static long f(int n)

{

if (n == 1) return 1;

if (n == 2) return 2;

if (m[n] != -1) return m[n];

return m[n] = f(n-1) + f(n-2) + 1;

}

public static void main(String[] args)

{

Arrays.fill(m, -1);

Scanner con = new Scanner(System.in);

int n = con.nextInt();

System.out.println(f(n));

con.close();

}

}