6008. Обратные треугольные числа

Треугольным числом называется число, которое может быть представлено в виде множества точек, уложенных в равносторонний треугольник с n точками на каждой стороне. Ниже приведены несколько примеров таких треугольников и соответствующих им треугольных чисел:

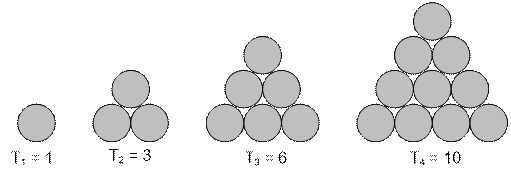
Легко заметить, что треугольное число является аддитивным аналогом факториала:

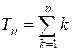
По заданному целому числу n определите, является ли оно треугольным. Если число треугольное, определите также количество точек на стороне соответствующего треугольника.

Например, если n = 10, программа должна сообщить, что это треугольное число с 4 точками на стороне, так как

10 = 4 + 3 + 2 + 1

Если n = 11, программа должна сообщить, что это не треугольное число.

Вход. Каждая строка содержит одно целое число n (0 < n < 10⁹). Последняя строка содержит -1 и не обрабатывается.

Выход. Для каждого значения n определите, является ли оно треугольным числом. Если да, выведите в отдельной строке количество точек на стороне. В противном случае выведите строку “bad”.

Пример входа	Пример выхода
55 1 91 587 499500 -1	Case 1: 10 Case 2: 1 Case 3: 13 Case 4: bad Case 5: 999

РЕШЕНИЕ

комбинаторика

Анализ алгоритма

Пусть k – количество точек на стороне равностороннего треугольника. Тогда общее число точек, необходимых для его полной укладки, равно сумме первых k натуральных чисел:

1 + 2 + … + k =

Такие числа называются треугольными.

Пусть задано целое число n – количество имеющихся точек. Необходимо определить, существует ли такое целое k > 0, для которого

= n

Умножим обе части уравнения на 2 и приведём его к стандартному квадратному виду:

k² + k – 2n = 0

Это квадратное уравнение относительно k. Оно имеет целочисленное решение тогда и только тогда, когда его дискриминант является полным квадратом. Дискриминант равен

d = 1 + 8n

Следовательно, число n является треугольным тогда и только тогда, когда значение d = 1 + 8n является полным квадратом. В этом случае положительный корень уравнения задаётся формулой

k =

Если найденное значение k является положительным целым числом, то число n треугольное, а k – количество точек на стороне треугольника. В противном случае число n не является треугольным.

Пример

Рассмотрим n = 55. Подставим это значение в уравнение:

k² + k – 110 = 0

Вычислим дискриминант:

d = 1 + 440 = 441

Так как 441 = 21² – полный квадрат, уравнение имеет целочисленное решение. Положительный корень равен

k = = = 10

Следовательно, число 55 является треугольным и соответствует треугольнику с 10 точками на стороне.

Реализация алгоритма

Последовательно обрабатываем тесты. Читаем входное значение n.

cs = 1;

while (scanf("%lld", &n), n != -1)

{

printf("Case %d: ", cs++);

Вычисляем дискриминант квадратного уравнения d.

d = 1 + 8 * n;

Проверяем, является ли дискриминант полным квадратом. Для этого вычисляем sd = и проверяем равенство sd * sd = d. Если дискриминант не является полным квадратом, то выводим строку “bad”.

sd = (long long)sqrt(d);

if (sd * sd != d)

{

printf("bad\n");

continue;

}

Вычисляем и выводим положительный корень уравнения.

k = (-1 + sqrt(d)) / 2;

printf("%lld\n", k);

}