6032. Шахматы
Слон – это
шахматная фигура, которая ходит только по диагонали. Известно, что слоны могут
добраться только до клеток одного цвета, причем до каждой из них за несколько
ходов (считаем что на доске нет других фигур). На доске заданы две клетки.
Определить, может ли слон достичь одну из них из другой, и каким образом.
Координаты в шахматах задаются буквой (от 'A' до 'H') и цифрой (от 1 до 8).
Буква задает колонку, а цифра строку доски. Шахматная доска, слон и поля,
достижимые за один ход:

Вход. Первая
строка содержит количество тестов. Каждый тест начинается со строки, содержащей
начальную позицию X и конечную позицию Y. Каждая позиция задается двумя
символами, разделенными пробелом. Буква задает колонку, а число строку. Входные
данные не содержат одинаковых тестов.
Выход. Для
каждого теста вывести одну строку. Если переместить слона из X в Y за любое
число ходов невозможно, то вывести "Impossible". Иначе вывести одну
из возможных последовательностей ходов от X до Y. Сначала вывести число ходов n (не более 4). Далее вывести n + 1 позицию, описывающих путь слона.
Все символы следует разделять одним пробелом. Существует много решений. Любое
из них, содержащее не более 4 ходов, допустимо. Напомним, что ходом называется
изменение позиции шахматной фигурой (в нашем случае слоном) согласно шахматным
правилам (то есть две соседние позиции в выводимой последовательности должны
быть разными).
|
Пример входа |
Пример выхода |
|
3 E 2 E 3 F 1 E 8 A |
Impossible 2 F 1 B 5 E 8 0 A 3 |
РЕШЕНИЕ
математика
Анализ алгоритма
Пусть (x1, y1) – начальное, (x2,
y2) – конечное поле.
Рассмотрим следующие варианты:
·
если поля (x1,
y1) и (x2, y2) совпадают, то слона перемещать не нужно.
·
слона нельзя переместить, если поля имеют разный цвет.
Это имеет место, когда сумма x1
+ y1 + x2 + y2 нечетная.
·
поля (x1,
y1) и (x2, y2) находятся на одной диагонали, если |x1 – x2| = |y1
– y2|. В этом случае
достаточно совершить одного хода.
·
в остальных случаях всегда достаточно совершить два
хода.
Рассмотрим,
как переместить слона из (x1,
y1) в (x2, y2) за два хода. Пусть для этого первым будет ход из (x1, y1) в (x0,
y0), а затем из (x0, y0) в (x2,
y2). В таком случае
координаты (x1, y1) и (x0, y0),
а также (x0, y0) и (x2, y2)
будут находиться на одной диагонали, следовательно
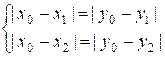
Система
уравнений эквивалентна совокупности двух систем:
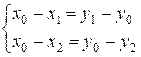 и
и 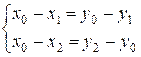 ,
,
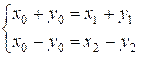 и
и 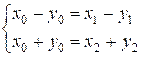 ,
,
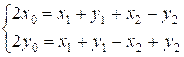 и
и 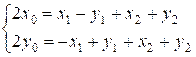 ,
,
откуда
получаются два возможных решения. Осталось проверить принадлежность этих
решений шахматной доске, то есть чтобы они не выходили за ее пределы.
Реализация алгоритма
Читаем
входные данные.
scanf("%d\n",&tests);
while(tests--)
{
scanf("%c %d %c %d\n",&a,&y1,&b,&y2);
Преобразуем символьные координаты в числовые. Слона с
поля (x1, y1) следует переместить на
поле (x2, y2).
x1 = a - 'A' + 1;
x2 = b - 'A' + 1;
Если начальное и конечное поля совпадают, то ходов
делать не требуется.
if ((x1 == x2) && (y1 == y2)) printf("0 %c %d\n",a,y1); else
Если поля имеют разный цвет, то перемещение слона
невозможно.
if ((x1 + y1 + x2 + y2) % 2 == 1) printf("Impossible\n"); else
Проверим, можно ли требуемое перемещение слона
совершить за один ход.
if (abs(x1 - x2) == abs(y1 - y2))
printf("1 %c %d %c %d\n",a,y1,b,y2);
else
{
Слона можно переместить за два хода. Вычисляем один из
возможных ответов (x0, y0).
x0 = x1 + y1 + x2
- y2; x0 /= 2;
y0 = x1 + y1 - x2
+ y2; y0 /= 2;
Если точка (x0,
y0) лежит в пределах
шахматной доски, то она является искомой.
if (x0 >= 1 && x0 <= 8 && y0
>= 1 && y0 <= 8)
printf("2 %c %d %c %d %c %d\n",a,y1,x0 + 'A' - 1,y0,b,y2);
else
{
Иначе ответом является второе решение.
x0 = x1 - y1 +
x2 + y2; x0 /= 2;
y0 = x2 + y2 -
x1 + y1; y0 /= 2;
printf("2 %c %d %c %d %c %d\n",a,y1,x0 + 'A' - 1,y0,b,y2);
}
}
}