6033. Пробег

Один раз в год Джо и его друзья хотят посетить местную ярмарку в Эрлангене, называемую Бергкирхвайх. В этом году они хотят совершить Kastenlauf (box run). Они стартуют от дома Джо, имея одну коробку (Kasten) пива с двадцатью бутылками. Чтобы их не мучила жажда, они пьют одну бутылку пива каждые 50 метров.

Поскольку путь от дома Джо к Бергкирхвайх довольно долгий, они должны потребить больше пива, чем взяли изначально. К счастью на пути имеются магазины, торгующие пивом. Когда они посещают магазин, то могут отказаться от своих пустых бутылок и купить новые, однако общее количество полных бутылок должно быть не больше двадцати (ребята слишком ленивы, чтобы нести более одной полной коробки).

Вам заданы координаты магазинов, дома Джо и расположения Бергкирхвайх. Напишите программу, которая определит, смогут ли Джо и его друзья счастливо добраться до Бергкирхвайх, или же пиво закончится на их пути.

Вход. Первая строка содержит количество тесов t (t ≤ 50). Каждая строка начинается количеством магазинов n (0 ≤ n ≤ 100), торгующих пивом. Следующие n + 2 строки содержат (именно в таком порядке) местоположение дома Джо, магазинов и Бергкирхвайх. Местоположение задается двумя целочисленными координатами x и y (в метрах, -32768 ≤ x, y ≤ 32767). Поскольку Эрланген представляет собой город в виде прямоугольной сетки, то расстояние между двумя точками равно сумме разностей координат (Манхетенская метрика).

Выход. Для каждого теста вывести в отдельной строке либо "happy" (если Джо и его друзья благополучно достигнут Бергкирхвайха), или "sad" (если у них на пути закончится пиво).

Пример входа	Пример выхода
2 2 0 0 1000 0 1000 1000 2000 1000 2 0 0 1000 0 2000 1000 2000 2000	happy sad

РЕШЕНИЕ

графы – поиск в глубину

Анализ алгоритма

Поскольку количество бутылок, которое ребята могут нести с собой, равно 20, а через каждые 50 метров следует выпить одну бутылку, то перемещаться они смогут только между магазинами, расстояние между которыми не более 20 * 50 = 1000 метров.

Построим граф, вершинами которого будут дом Джо, магазины и Бергкирхвайх. Ребро между вершинами присутствует если только расстояние между ними не более 1000 метров. То есть неориентированные ребра указывают возможные пути передвижения Джо и его друзей.

Запускаем поиск в глубину из дома Джо. Если из нее можно достичь Бергкирхвайх, то друзья будут счастливы, иначе – нет.

Пример

Для первого и второго примеров граф будет выглядеть следующим образом:

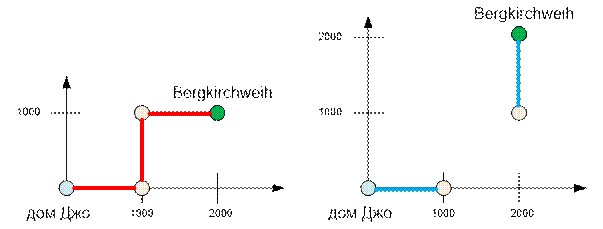
В первом примере Джо с друзями могут достичь ярмарку Бергкирхвайх. Во втором – нет. Передвигаться можно только между теми вершинами графа, расстояние между которыми не больше 1000 метров.

Реализация алгоритма

Координаты магазинов храним в (x[i], y[i]). Объявим граф передвижения g.

#define MAX 110

int x[MAX], y[MAX];

vector<vector<int> > g;

vector<int> used;

Поиск в глубину из вершины v.

void dfs(int v)

{

used[v] = 1;

for(int i = 0; i < g[v].size(); i++)

{

int to = g[v][i];

if (!used[to]) dfs(to);

}

}

Основная часть программы. Читаем входные данные.

scanf("%d",&tests);

while(tests--)

{

scanf("%d",&n);

Поскольку входные данные содержат несколько тестов, то очищаем массивы.

g.clear(); g.resize(n+2);

used.clear(); used.resize(n+2);

Читаем координаты дома Джо (x[0], y[0]), магазинов и Бергкирхвайх (x[n – 1], y[n – 1]).

for(i = 0; i < n + 2; i++)

scanf("%d %d",&x[i],&y[i]);

Строим граф возможных передвижений. Из вершины (x[i], y[i]) можно перейти в вершину (x[j], y[j]) если только расстояние между ними не более 1000 метров. Граф неориентированный. Метрика манхетенская.

for(i = 0; i < n + 2; i++)

for(j = i + 1; j < n + 2; j++)

if (abs(x[i] - x[j]) + abs(y[i] - y[j]) <= 1000)

{

g[i].push_back(j);

g[j].push_back(i);

}

Стартуем из дома Джо. Запускаем поиск в глубину из вершины 0.

dfs(0);

Если Бергкирхвайх достижим, то выводим “happy”, иначе выводим “sad”.

if (used[n + 1]) puts("happy");

else puts("sad");

}

Реализация – матрица смежности

#include <stdio.h>

#include <string.h>

#define MAX 110

int tests, n, i, j;

int x[MAX], y[MAX];

int g[MAX][MAX], used[MAX];

int abs(int x)

{

return (x < 0) ? -x : x;

}

void dfs(int v)

{

used[v] = 1;

for(int i = 0; i < n + 2; i++)

if (g[v][i] && !used[i]) dfs(i);

}

int main(void)

{

scanf("%d",&tests);

while(tests--)

{

scanf("%d",&n);

memset(g,0,sizeof(g));

memset(used,0,sizeof(used));

// 0 = Jo's house, start

// 1 .. n - stores selling beer

// n+1 - Bergkirchweih, finish

for(i = 0; i < n + 2; i++)

scanf("%d %d",&x[i],&y[i]);

for(i = 0; i < n + 2; i++)

for(j = i + 1; j < n + 2; j++)

if (abs(x[i] - x[j]) + abs(y[i] - y[j]) <= 1000)

g[i][j] = g[j][i] = 1;

// Start from Jo's house

dfs(0);

// if Bergkirchweih is reached, then happy

if (used[n + 1]) puts("happy");

else puts("sad");

}

return 0;

}