6033. Kastenlauf

Once every year, Jo and his friends want to visit the local fair in Erlangen, called Bergkirchweih. This year, they want to make a Kastenlauf (box run). They start at Jo’s home and have one box (Kasten) of beer (with twenty bottles). As they are very thirsty, they drink one bottle of beer every 50 meters.

As the way from Jo's home to the Bergkirchweih is pretty long, they need more beer than they have initially. Fortunately, there are stores selling beer on the way. When they visit a store, they can drop their empty bottles and buy new bottles, but their total number of full bottles will not be more than twenty (because they are too lazy to carry more than one full box).

You are given the coordinates of the stores, of Jo's home and of the location of the Bergkirchweih. Write a program to determine whether Jo and his friends can happily reach the Bergkirchweih, or whether they will run out of beer on the way.

Input. First line contains the number of test cases t (t ≤ 50). Each test case starts with one line, containing the number n (0 ≤ n ≤ 100) of stores selling beer. The next n + 2 lines contain (in this order) the location of Jo’s home, of the stores, and of the Bergkirchweih. The location is given with two integer coordinates x and y (both in meters, -32768 ≤ x, y ≤ 32767). As Erlangen is a rectangularly laid out city, the distance between two locations is the difference of the first coordinate plus the difference of the second coordinate (also called Manhattan-Metric).

Output. For each test case print one line, containing either “happy” (if Jo and his friends can happily reach the Bergkirchweih), or “sad” (if they will run out of beer on the way).

Sample input	Sample output
2 2 0 0 1000 0 1000 1000 2000 1000 2 0 0 1000 0 2000 1000 2000 2000	happy sad

SOLUTION

graphs – depth first search

Algorithm analysis

Since the number of bottles that guys can carry with them is 20, and every 50 meters one should drink one bottle, they can only move between stores, the distance between which is no more than 20 * 50 = 1000 meters.

Let’s build a graph with Joe’s house, shops and Bergkirchweich as its vertices. An edge between the vertices is present if only the distance between them is not more than 1000 meters. That is, the undirected edges indicate the possible paths of movement for Joe and his friends.

Start the depth first search from the Joe’s house. If it is possible to reach Bergkirchweich from it, then friends will be happy, otherwise they will not.

Example

For the first and the second examples, the graph will look like this:

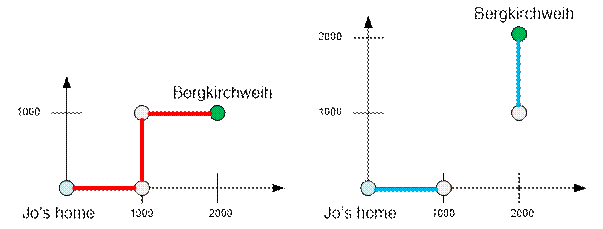
In the first example, Joe and his friends can reach the Bergkirchweich fair. In the second, no. You can only move between those vertices of the graph, the distance between which is no more than 1000 meters.

Algorithm realization

Store the coordinates in (x[i], y[i]). Declare the movement graph g.

#define MAX 110

int x[MAX], y[MAX];

vector<vector<int> > g;

vector<int> used;

Depth first search from the vertex v.

void dfs(int v)

{

used[v] = 1;

for(int i = 0; i < g[v].size(); i++)

{

int to = g[v][i];

if (!used[to]) dfs(to);

}

}

The main part of the program. Read the input data.

scanf("%d",&tests);

while(tests--)

{

scanf("%d",&n);

Since the input data contains several tests, clear the arrays.

g.clear(); g.resize(n+2);

used.clear(); used.resize(n+2);

Read the coordinates of Jo’s home (x[0], y[0]), shops and Bergkirchweih (x[n – 1], y[n – 1]).

for(i = 0; i < n + 2; i++)

scanf("%d %d",&x[i],&y[i]);

Build a graph of possible movements. From the vertex (x[i], y[i]) you can go to the vertex (x[j], y[j]) if only the distance between them is no more than 1000 meters. The graph is undirected. The metric is Manhattan.

for(i = 0; i < n + 2; i++)

for(j = i + 1; j < n + 2; j++)

if (abs(x[i] - x[j]) + abs(y[i] - y[j]) <= 1000)

{

g[i].push_back(j);

g[j].push_back(i);

}

Start from Joe’s house. Start the depth first search from the vertex 0.

dfs(0);

If Bergkirchweich is reachable, then output “happy”, otherwise output “sad”.

if (used[n + 1]) puts("happy");

else puts("sad");

}

Algorithm realization – adjacency matrix

#include <stdio.h>

#include <string.h>

#define MAX 110

int tests, n, i, j;

int x[MAX], y[MAX];

int g[MAX][MAX], used[MAX];

int abs(int x)

{

return (x < 0) ? -x : x;

}

void dfs(int v)

{

used[v] = 1;

for(int i = 0; i < n + 2; i++)

if (g[v][i] && !used[i]) dfs(i);

}

int main(void)

{

scanf("%d",&tests);

while(tests--)

{

scanf("%d",&n);

memset(g,0,sizeof(g));

memset(used,0,sizeof(used));

// 0 = Jo's house, start

// 1 .. n - stores selling beer

// n+1 - Bergkirchweih, finish

for(i = 0; i < n + 2; i++)

scanf("%d %d",&x[i],&y[i]);

for(i = 0; i < n + 2; i++)

for(j = i + 1; j < n + 2; j++)

if (abs(x[i] - x[j]) + abs(y[i] - y[j]) <= 1000)

g[i][j] = g[j][i] = 1;

// Start from Jo's house

dfs(0);

// if Bergkirchweih is reached, then happy

if (used[n + 1]) puts("happy");

else puts("sad");

}

return 0;

}