6082. Супернатуральное
Натуральное
число будем называть супернатуральным, если в своем десятичном виде оно не
содержит единиц, а произведение всех его цифр равно n. Для заданного n
выясните, сколько существует супернатуральных чисел.
Вход. Содержит одно
целое число n, не превосходящее
2×109.
Выход. Вывести
количество супернатуральных чисел по модулю 101.
|
Пример
входа |
Пример
выхода |
|
6 |
3 |
РЕШЕНИЕ
рекурсия
Анализ алгоритма
Обозначим через
f(n) количество супернатуральных
чисел.
Если n = 1, то ответ 0. Потому что не существует
натурального числа, не содержащего единиц в десятичной записи и произведение
цифр которого равно 1. То есть f(1) = 0.
Если n простое и меньше 10, то f(n) = 1
(супернатуральными являются простые числа 2, 3, 5, 7). Если n простое и больше 10, то f(n) = 0, так как n не имеет делителей от 2 до 9.
Для подсчета f(n) необходимо перебрать все делители d от 2 до 9 (цифры в числе могут быть только от 2 до
9) числа n и просуммировать значения f(n / d):
f(n) = 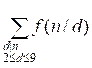
Пример
Произведение
цифр следующих трех натуральных чисел равно 6: 6, 23 и 32.
При n = 8 имеются четыре супернатуральных
числа: 222, 24, 42 и 8.
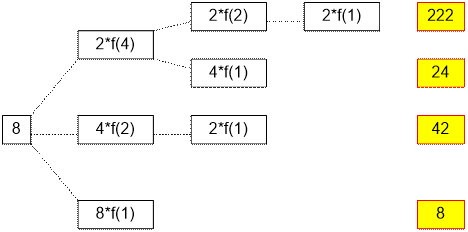
При построении
самих супернатуральных чисел операция умножения трактуется как конкатенация
символов, а f(1) считается пустым символом.
Реализация алгоритма
Будем проводить
вычисление функции f с запоминанием ее значений в отображении m. То есть
значение f(n) запомним в m[n].
map<int,int> m;
Функция f(n) вычисляет количество супернатуральных
чисел, произведение цифр которых равно n, и запоминает его в m[n].
int f(int
n)
{
int res = 0;
if (m[n]) return m[n];
for(int i = 2; i <= 9; i++)
if (n % i
== 0) res = (res + f(n/i)) % 101;
return m[n] =
res;
}
Основная часть программы. Читаем
входные данные, вычисляем и выводим ответ.
scanf("%d",&n);
m[1] = 1;
res = (n == 1) ?
0 : f(n);
printf("%d\n",res);
Python реализация
memo = {1:1}
def f(n):
res = 0
if not n in memo:
for i in range(2,10) :
if (n % i == 0) :
res = (res +
f(n // i)) % 101
memo[n] = res
return memo[n]
n = int(input())
if (n == 1) :
res = 0
else :
res = f(n)
print(res)