6198. Минимальная сумма
Имеются два
массива натуральных чисел a1..n и b1..n. Найдите
перестановку i1, i2, ..., in чисел 1, 2, ..., n,
для которой сумма
a1 * bi1
+ ... + an * bin
минимальна. В
перестановку каждое число должно входить только один раз.
Вход. В первой строке
находится количество элементов n (n ≤ 100) в массивах. Во второй
строке заданы значения элементов первого массива, а в третьей – второго.
Значения элементов массивов не превышают 106.
Выход. Выведите
минимальное значение искомой суммы.
|
Пример
входа |
Пример
выхода |
|
5 7 2 4 3 10 5 11 6 9 6 |
165 |
РЕШЕНИЕ
жадность
Анализ алгоритма
Рассмотрим случай массивов с двумя элементами. Пусть A = {p, q} (p < q), B = {x, y}. Рассмотрим условие, при котором сумма p * x + q * y
будет наименьшей. Рассмотрим два
варианта перестановок:
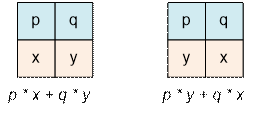
Неравенство p * x + q * y < p
* y + q * x имеет место,
если
x * (p – q) < y * (p – q)
Учитывая что p ≠ q, разделим неравенство на (p – q) <
0. Получим x > y.
То есть сумма p * x + q * y (при p < q) будет
минимальной, если x > y.
Рассмотрим пару элементов исходных массивов A и B. Если ai < aj,
bi < bj, то поменяв местами bi и bj, мы уменьшим общую сумму.
Отсортируем массив а
по возрастанию, а массив b по
убыванию. Тогда получим сумму с наименьшим значением
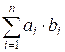
Пример
Вычислим сумму
для данных из примера.
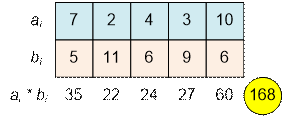
Возьмем пару для которой a1 < a5 и b1 < b5. Поменяем местами b1 и b5. Сумма
уменьшится.
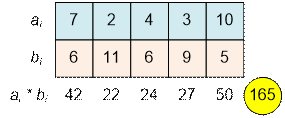
Для заданного примера для любой пары (i, j) выполняется: если ai < aj, то bi > bj. Следовательно текущая перестановка оптимальная.
Рассмотрим
получение минимальной суммы, отсортировав а
по возрастанию, а массив b по
убыванию.
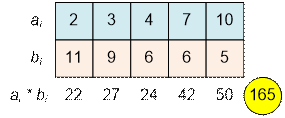
Реализация алгоритма
Объявим входные
массивы чисел.
#define MAX 101
int a[MAX], b[MAX];
Читаем входные данные.
scanf("%d",&n);
for(i = 0; i < n; i++)
scanf("%d",&a[i]);
for(i = 0; i < n; i++)
scanf("%d",&b[i]);
Сортируем первый массив по возрастанию, второй – по убыванию.
sort(a,a+n);
sort(b,b+n,greater<int>());
Вычисляем искомую минимальную сумму, значение которой может
быть 64-битовым целым.
res = 0;
for(i = 0; i < n; i++)
res += 1LL * a[i] *
b[i];
Выводим результат.
printf("%lld\n",res);
Реализация с динамическим
выделением памяти
#include <cstdio>
#include <algorithm>
#include <set>
using namespace std;
int i, n;
int *a, *b;
long long res;
int main(void)
{
scanf("%d",&n);
a = new int[n];
for(i = 0; i < n; i++)
scanf("%d",&a[i]);
b = new int[n];
for(i = 0; i < n; i++)
scanf("%d",&b[i]);
sort(a,a+n);
sort(b,b+n,greater<int>());
for(res = i = 0; i < n; i++)
res += 1LL * a[i] *
b[i];
printf("%lld\n",res);
delete[] a;
delete[] b;
return 0;
}
Java реализация
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
Integer a[] = new Integer[n];
for(int i = 0; i < n; i++)
a[i] = con.nextInt();
Integer b[] = new Integer[n];
for(int i = 0; i < n; i++)
b[i] = con.nextInt();
Arrays.sort(a);
Arrays.sort(b,Collections.reverseOrder());
long res = 0;
for(int i = 0; i < n; i++)
res += 1L * a[i] * b[i];
System.out.println(res);
con.close();
}
}
Python реализация
Читаем входные
данные.
n = int(input())
l1 = list(map(int,input().split()))
l2 = list(map(int,input().split()))
Сортируем первый
массив по возрастанию, второй – по убыванию.
l1.sort()
l2.sort(reverse = True)
Вычисляем искомую
минимальную сумму.
res = 0
for i in range(n):
res +=
l1[i] * l2[i]
Выводим
результат.
print(res)