6249. Planting Trees

Farmer Jon has recently bought n tree seedlings that he wants to plant in his yard. It takes 1 day to plant a seedling, and for each tree, Jon knows exactly how many days after planting it will take to reach full maturity. Jon would also like to throw a party for his farmer friends, but in order to impress them, he would like to organize the party only after all the trees have grown. More precisely, the party can be organized at the earliest the next day after the last tree has grown up.

Help Jon find out the earliest day the party can take place. Jon can choose the order of planting the trees as he likes, so he wants to plant the trees in such a way that the party will be as soon as possible.

Input. The first line contains a single integer n (1 ≤ n ≤ 10⁵) denoting the number of seedlings. Then a line with n integers t_i (1 ≤ t_i ≤ 10⁶) follows, where t_i denotes the number of days it takes for the i-th tree to grow.

Output. Print one integer, denoting the earliest day when the party can be organized. The days are numbered 1, 2, 3, ... starting from the current moment.

Sample input	Sample output
4 2 3 4 3	7

SOLUTION

greedy

Algorithm analysis

It is beneficial to plant the tree that grows the longest first. Sort the growth times of the trees in descending order – in this order we’ll plant them.

Let John plant a tree on the i-th day that will grow for t_i days. This means that the tree will grow from the (i + 1)-th day to the (i + t_i)-th. If the i-th tree is the last to grow, then the party can be held on the (i + t_i + 1)-th day. It remains to find the maximum among these values, which will be the answer:

Example

From the left, consider the case if we’ll plant the trees in the order 2, 3, 3, 4. From the right, consider the case when trees are planted in a decreasing (optimal) order of their growth time. The day the tree was planted is marked in blue.

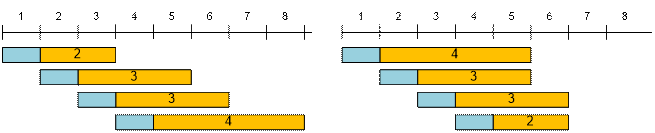
With the optimal planting of four trees, a party can be held on day number , which equals

max(1 + 4 + 1, 2 + 3 + 1, 3 + 3 + 1, 4 + 2 + 1) = max(6, 6, 7, 7) = 7

Algorithm realization

The comparator f sorts the array in descending order.

int f(int a, int b)

{

return a > b;

}

The main part of the program. Read the input data. Vector t contains the number of days in which the existing trees will grow. Since the days are numbered from 1, we will store numbers in the array t starting from index 1.

scanf("%d",&n);

t.resize(n+1);

for(i = 1; i <= n; i++)

scanf("%d",&t[i]);

Sort the growth times of the trees in descending order.

sort(t.begin()+1,t.end(),f);

Find the earliest day res when it will be possible to host a party.

res = 0;

for(i = 1; i <= n; i++)

res = max(res,i + t[i] + 1);

Print the answer.

printf("%d\n",res);

Java realization

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

Integer t[] = new Integer[n+1];

t[0] = 2000000000;

for(int i = 1; i <= n; i++)

t[i] = con.nextInt();

Arrays.sort(t, Collections.reverseOrder());

int res = 0;

for(int i = 1; i <= n; i++)

res = Math.max(res, i + t[i] + 1);

System.out.println(res);

con.close();

}

}