6263. Башня
карликов
Маленький
Вася играет в игру “Башня
карликов”. В этой игре имеется n различных предметов, которые можно надеть на персонажа – карлика. Все предметы пронумерованы от 1 до n. Вася
хочет получить предмет под номером 1.
Существует
два способа получения предметов:
·
Купить предмет: i-ый
предмет стоит ci денег.
· Сконструировать предмет: в игре доступно m различных рецептов. Чтобы сконструировать новый предмет,
нужно отдать два других разных предмета.
Помогите
Васе потратить как можно меньше денег, чтобы получить предмет номер 1.
Вход. Первая
строка содержит два числа n и m (1 ≤ n ≤ 104, 0 ≤ m ≤ 105) – количество различных предметов и число рецептов конструирования.
Вторая
строка содержит n целых чисел ci (0 ≤ ci ≤ 109) –
стоимости предметов.
Каждая из
следующих m строк описывает один
рецепт. В каждой строке записаны три различных целых числа ai, xi, yi,
где ai – предмет, который можно сконструировать из предметов xi и yi (1 ≤ ai,
xi, yi ≤ n, ai ≠ xi, xi ≠ yi,
yi ≠ ai).
Выход. Выведите одно число – минимальное количество
денег, которое необходимо потратить.
|
Пример входа 1 |
Пример выхода 1 |
|
5 3 5 0 1 2 5 5 2 3 4 2 3 1 4 5 |
2 |
|
|
|
|
Пример входа 2 |
Пример выхода 2 |
|
3 1 2 2 1 1 2 3 |
2 |
РЕШЕНИЕ
жадность
Анализ алгоритма
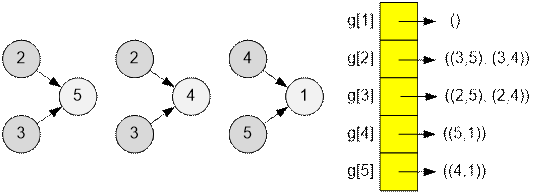
Построим
граф в виде списка смежности g, где g[i] содержит пары чисел (j, a) такие
что из предметов i и j можно сконструировать
предмет a: (i, j) → a.
Пусть cost – массив, изначально содержащий стоимость покупки
предметов (cost[i] = ci). В конце работы алгоритма
cost[i] будет содержать минимальное количество денег, необходимое для
получения предмета i.
Изначально все предметы считаются необработанными (used[i] = 0).
Пока существует хотя бы один необрабротанный предмет:
·
Находим предмет a с наименьшей стоимостью;
·
Применяем все правила, перечисленные в g[a];
·
Отмечаем предмет a как обработанный: used[a] = 0;
Для
каждого правила (a, b) →
to из g[a] пересчитываем
cost[to]
= min(cost[to], cost[a]
+ cost[b])
Пример
Рассмотрим
первый тест. Имеется 5 предметов со следующими стоимостями их покупки:

Имеются
три правила конструирования предметов. Построим на их основе список смежности.
Предмет 2
имеет наименьшую стоимость cost[2] =
0. Применяем все правила, в которых участвует предмет 2, а именно те, что
перечислены в g[2]. После
этого отмечаем предмет 2 как обработанный.
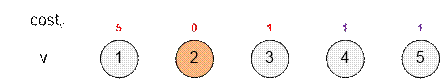
Следующим
необработанным предметом с наименьшей стоимостью будет 3. Применяем правила,
перечисленные в g[3]. Стоимости предметов при этом не изменяются.

Далее
необработанным предметом с наименьшей стоимостью становится предмет 4.
Применяем правило из g[4].

В
последующих операциях стоимости предметов не меняются. Таким образом,
минимальная стоимость получения предмета 1 равна 2.
Реализация алгоритма
Объявим
рабочие массивы. Объявим список смежности g, который будет содержать правила конструирования
предметов.
vector<int> cost, used;
vector<vector<pair<int, int>>> g;
Читаем входные данные. Инициализируем массивы.
scanf("%d %d", &n, &m);
g.resize(n
+ 1);
cost.resize(n
+ 1);
used.resize(n
+ 1);
Читаем
стоимости покупки предметов.
for (i = 1; i <= n; i++)
scanf("%d", &cost[i]);
Читаем правила
конструирования предметов и на их основе строим список смежности.
for (i = 0; i < m; i++)
{
scanf("%d %d %d", &a, &x, &y);
g[x].push_back(make_pair(y, a));
g[y].push_back(make_pair(x, a));
}
Совершаем n итераций.
for (k = 0; k < n; k++)
{
Среди необработанных предметов ищем тот, у которого
наименьшая стоимость. Пусть это будет предмет с номером a.
mn = 2e9; a = -1;
for (i = 1; i <= n; i++)
if (!used[i] && cost[i] < mn)
{
mn = cost[i];
a = i;
}
Отмечаем предмет a как обработанный.
used[a] = 1;
Перебираем все правила, в которых участвует предмет a.
for (auto x : g[a])
{
b = x.first;
to = x.second; // (a, b) -> to
if (cost[a] + cost[b] < cost[to]) cost[to] = cost[a] + cost[b];
}
}
Выводим минимальное количество денег, необходимое для
покупки первого предмета.
printf("%d\n", cost[1]);
Python реализация
В Python inf
– это специальное значение, которое обозначает бесконечность. Оно доступно в
модуле math и для использования модуль необходимо импортировать.
from math import inf
Читаем входные данные.
n, m = map(int, input().split())
cost = [0] + list(map(int, input().split()))
Инициализируем списки.
used = [False] * (n + 1)
g = [[] for _ in range(n + 1)]
Читаем правила
конструирования предметов и на их основе строим список смежности.
for _ in range(m):
a,
x, y = map(int, input().split())
g[x].append((y, a))
g[y].append((x, a))
Выполняем n итераций.
for k in range(n):
На каждой итерации среди необработанных предметов ищем
тот, у которого наименьшая стоимость. Пусть это будет предмет с номером a.
mn
= inf
a
= -1
for i in range(1, n + 1):
if not used[i] and cost[i] < mn:
mn = cost[i]
a = i
Отмечаем предмет a как обработанный.
used[a] = True
Перебираем все правила, в которых участвует предмет a.
for
b, to in g[a]:
if cost[a] +
cost[b] < cost[to]:
cost[to] = cost[a] + cost[b]
Выводим минимальное количество
денег, необходимое для покупки первого предмета.
print(cost[1])