6389. Порядок Штралера

В геологии речная система может быть представлена в виде ориентированного графа. Каждый отрезок реки представляется ребром; направление ребра совпадает с направлением течения реки. Вершинами являются истоки рек (например озеро или ручей), места слияния или расхождения рек, либо устья рек.

Порядок Штралера речной системы вычисляется следующим образом.

· порядок вершины – истока равен 1.

· для каждой другой вершины пусть i – наибольший порядок среди всех узлов, находящихся вверх по течению. Если только один из таких узлов имеет порядок i, тогда текущая вершина также имеет порядок i. Если два или более узла вверх по течению имеют порядок i, то порядок текущей вершины равен i + 1.

Порядок всей речной системы равен порядку вершины - устья. В приведенном примере речная система имеет только одно устье. Порядок Штралера равен трем (3).

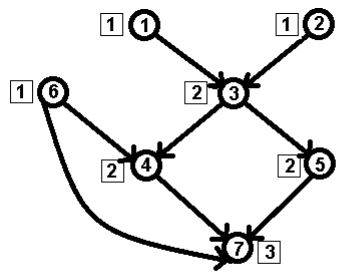
Число в прямоугольнике – порядок Штралера. Число в круге – номер вершины.

Напишите программу, которая определит порядок заданной речной системы.

Реальная река с наибольшим порядком – Амазонка, ее порядок равен 12. Река с наибольшим порядком в США – Миссисипи, ее порядок 10.

Вход. Первая строка содержит количество тестов t (1 ≤ t ≤ 1000). Каждый тест следует обработать независимо от других.

Каждый тест состоит из нескольких строк. Первая строка каждого теста содержит три натуральных числа k, m и p (2 ≤ m ≤ 1000). k - номер теста. m – количество вершин в графе, p - количество ребер. Далее следуют p строк, каждая из которых задает ребро графа. Строка содержит два натуральных числа a и b, указывающих что вода течет от a к b (1 ≤ a, b ≤ m). Вершина m – устье реки, у нее нет исходящих ребер.

Выход. Для каждого теста вывести одну строку. В ней вывести номер теста, пробел и порядок речной системы.

Пример входа	Пример выхода
1 1 7 8 1 3 2 3 6 4 3 4 3 5 6 7 5 7 4 7	1 3

РЕШЕНИЕ

графы – поиск в глубину

Анализ алгоритма

Построим ориентированный граф с обратными ребрами. Устье исходного графа будем считать истоком построенного, из него запустим поиск в глубину. В процессе поиска пересчитываем порядок Штралера order[v] для каждой вершины v как описано в условии задачи.

Рассмотрим вершину v. Пусть to₁, to₂, …, to_k – ее сыновья. Нам необходимо знать наибольший порядок Штралера среди сыновей, а также количество раз, которое он встречается среди них. Пусть структура map<int,int> mp; хранит пары (order, cnt) – порядок Штралера и количество раз, которое он встречается среди сыновей.

Например, у вершины 7 имеются три сына:

· вершина 6 с порядком Штралера 1;

· вершина 4 с порядком Штралера 2;

· вершина 5 с порядком Штралера 2;

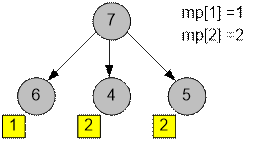
Вершина 7 среди своих сыновей имеет:

· одну вершину с порядком Штралера 1, следовательно mp[1] = 1;

· две вершины с порядком Штралера 2, следовательно mp[2] = 2;

Находим максимальный порядок Штралера среди сыновей вершины v.

· если он встречается только у одного сына to, то установим order[v] = order[to];

· если он встречается больше чем у одного сына, то установим order[v] = order[to] + 1;

Для вершины 7 максимальный порядок Штралера равен 2, и он достигается на двух вершинах: 4 и 5. Следовательно order[7] = order[4] + 1 = 2 + 1 = 3.

Реализация алгоритма

Обратный граф строим в списке смежности g. В order[i] будем вычислять порядок Штралера для i-ой вершины.

vector<vector<int> > g;

vector<int> order;

Функция dfs совершает поиск в глубину из вершины v и возвращает порядок Штралера для вершины v.

int dfs(int v)

{

Если порядок Штралера для вершины v уже посчитан, то вернем его.

if (order[v] > 0) return order[v];

Перебираем сыновей to вершины v. Нам необходимо найти наибольший порядок Штралера среди сыновей, а также количество раз, которое он встречается среди них. В структуре mp храним пары (order, cnt) – порядок Штралера и количество раз, которое он встречается среди сыновей to.

int suns = 0, mx = 0;

map<int,int> mp;

for(int i = 0; i < g[v].size(); i++)

{

int to = g[v][i];

mp[dfs(to)]++;

}

Если вершина v (v является листом) не имеет сыновей, то порядок равен 1.

if (mp.empty())

order[v] = 1;

else

{

Установим итератор iter на пару с максимальным порядком Штралера.

map<int,int>::iterator iter = mp.end();

iter--;

Если максимальный порядок достигается только на одном сыне, то порядок v равен порядку этого сына.

if ((*iter).second == 1)

order[v] = (*iter).first;

else

Иначе порядок v равен порядку этого сына, увеличенного на 1.

order[v] = (*iter).first + 1;

}

return order[v];

}

Основная часть программы. Читаем входные данные. Строим обратный граф. Для каждого исходного ребра u → v заносим в наш граф ребро v → u.

scanf("%d", &tests);

for(i = 1; i <= tests; i++)

{

scanf("%d %d %d",&k,&m,&p);

g.clear(); g.resize(m + 1);

order.clear(); order.resize(m + 1);

for(j = 1; j <= p; j++)

{

scanf("%d %d",&u,&v);

g[v].push_back(u);

}

Запускаем поиск в глубину из устья реки – вершины m и выводим ее порядок вместе с номером теста.

res = dfs(m);

printf("%d %d\n",i,res);

}