6576. Road

In a certain country, there are n roads numbered from 1 to n. A civil engineer must build a public road network that connects all cities, meaning it must be possible to travel from any city to any other, possibly via intermediate cities. His team has surveyed several routes (roads between pairs of cities). Each road is bidirectional. Building a road requires certain costs: the shorter the route, the cheaper the construction.

The engineer has never planned a road network in advance. He simply chooses a road he likes and builds it until all cities are connected.

Now the engineer wants to build a road between cities p and q. Under pressure from the government, aiming to reduce expenses, he asks you to write a program that determines whether it is worth building this road. Your program should print “YES” if, after construction, the road (p, q) will be part of the minimum road network connecting all cities. Otherwise, it should print “NO”.

Input. The first line contains the number of test cases t (t≤10).

Each test case begins with a line containing four integers n, m, p, and q. Here n (2 ≤ n ≤ 10000) is the number of cities, m (1 ≤ m ≤ 20000) is the number of roads, and p and q (1 ≤ p, q ≤ n) specify the cities between which the engineer intends to build a road.

The next m lines each contain three integers u, v, and w (1 ≤ u, v ≤ n, 1 ≤ w ≤ 4⋅10⁵) describing an existing bidirectional road of length w between cities u and v. All road lengths are distinct. There can be at most one road between any pair of cities. It is guaranteed that the graph is connected, i.e., there is a path between any pair of cities. All numbers are integers.

Output. For each test case, print “YES” if the road (p, q) will be part of the minimum road network. Otherwise, print “NO”.

Sample input	Sample output
3 2 1 1 2 1 2 4 3 3 2 3 1 2 1 1 3 2 2 3 3 4 5 3 4 1 2 1 1 3 3 3 4 2 1 4 4 4 2 5	YES NO YES

SOLUTION

graphs – Kruskal algorithm

Algorithm analysis

Run Kruskal’s algorithm on the initial graph. In the set s, store the edges that belong to the minimum spanning tree. Next, check whether the given edge (p, q) is part of this spanning tree. To do this, we need to verify whether the pair (p, q) or (q, p) is contained in the set s.

Example

The graphs given in the examples have the following form:

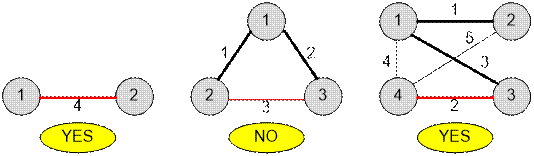
Algorithm implementation

Define a structure for a graph edge that contains a pair of vertices and the edge weight. Define an array of edges e.

struct Edge

{

int u, v, dist;

};

vector<Edge> e;

Define an array parent, which is used to implement the disjoint set union structure.

vector<int> parent;

The function Repr finds the representative of the set to which vertex n belongs.

int Repr(int n)

{

while(n != parent[n]) n = parent[n];

return n;

}

The function Union merges the sets containing the elements x and y.

int Union(int x, int y)

{

x = Repr(x); y = Repr(y);

if (x == y) return 0;

parent[y] = x;

return 1;

}

The function lt serves as a comparator for sorting the edges.

int lt(Edge a, Edge b)

{

return (a.dist < b.dist);

}

The main part of the program. Process several test cases.

scanf("%d", &tests);

while (tests--)

{

Read the input data. Initialize the parent array.

scanf("%d %d %d %d", &n, &m, &p, &q);

parent.resize(n + 1);

for (i = 1; i <= n; i++) parent[i] = i;

Read the graph edges.

e.resize(m);

for (i = 0; i < m; i++)

scanf("%d %d %d", &e[i].u, &e[i].v, &e[i].dist);

Sort the graph edges in ascending order of their weights.

sort(e.begin(), e.end(), lt);

For each test case, reset the variable flag. It takes the value 1 or 0 depending on whether the edge (p, q) belongs to the minimum spanning tree.

flag = 0;

Run Kruskal’s algorithm to construct the minimum spanning tree. If the edge (e[i].u, e[i].v) is included in the spanning tree, check whether it matches the edge (p, q).

for (i = 0; i < m; i++)

if (Union(e[i].u, e[i].v))

It is necessary to check two conditions: (e[i].u, e[i].v) = (p, q) and (e[i].u, e[i].v) = (q, p).

if ((e[i].u == p && e[i].v == q) ||

(e[i].u == q && e[i].v == p))

{

If the edge (e[i].u, e[i].v) matches (p, q) or (q, p), set flag = 1 and break the loop.

flag = 1;

break;

}

Depending on the value of the variable flag, print the answer.

if (flag)

puts("YES");

else

puts("NO");

}

Algorithm implementation – set

Define a structure for a graph edge that contains a pair of vertices and the edge weight. Define an array of edges e.

struct Edge

{

int u, v, dist;

};

vector<Edge> e;

Define an array parent, which is used to implement the disjoint set union structure.

vector<int> parent;

In the set s, store the edges that belong to the minimum spanning tree.

set<pair<int, int> > s;

The function Repr finds the representative of the set to which vertex n belongs.

int Repr(int n)

{

while(n != parent[n]) n = parent[n];

return n;

}

The function Union merges the sets containing the elements x and y.

int Union(int x, int y)

{

x = Repr(x); y = Repr(y);

if (x == y) return 0;

parent[y] = x;

return 1;

}

The function lt serves as a comparator for sorting the edges.

int lt(Edge a, Edge b)

{

return (a.dist < b.dist);

}

The main part of the program. Process several test cases.

scanf("%d", &tests);

while (tests--)

{

Read the input data. Initialize the parent array.

scanf("%d %d %d %d", &n, &m, &p, &q);

parent.resize(n + 1);

for (i = 1; i <= n; i++) parent[i] = i;

Read the graph edges.

e.resize(m);

for (i = 0; i < m; i++)

scanf("%d %d %d", &e[i].u, &e[i].v, &e[i].dist);

Sort the graph edges in ascending order of their weights.

sort(e.begin(), e.end(), lt);

For each test case, clear the set s.

s.clear();

Run Kruskal’s algorithm to construct the minimum spanning tree. If the edge (e[i].u, e[i].v) is included in the spanning tree, add it to the set s.

for (i = 0; i < m; i++)

if (Union(e[i].u, e[i].v)) s.insert(make_pair(e[i].u, e[i].v));

After the algorithm finishes, check whether the given edge (p, q) belongs to the minimum spanning tree. To do this, we need to determine whether the pair (p, q) or (q, p) is contained in the set s.

if ((s.find(make_pair(p, q)) != s.end()) ||

(s.find(make_pair(q, p)) != s.end()))

puts("YES");

else

puts("NO");

}

Java implementation

import java.util.*;

class Edge

{

int u, v, dist;

Edge (int u, int v, int dist)

{

this.u = u;

this.v = v;

this.dist = dist;

}

};

class Pair

{

int u, v;

Pair (int u, int v)

{

this.u = u;

this.v = v;

}

};

public class Main

{

static int mas[];

static int size[];

static int Repr(int n)

{

if (n == mas[n]) return n;

return mas[n] = Repr(mas[n]);

}

static int Union(int x,int y)

{

x = Repr(x); y = Repr(y);

if(x == y) return 0;

if (size[x] < size[y])

{

int temp = x; x = y; y = temp;

}

mas[y] = x;

size[x] += size[y];

return 1;

}

public static class MyFun implements Comparator<Edge>

{

public int compare(Edge a, Edge b)

{

return a.dist - b.dist;

}

}

public static class PairFun implements Comparator<Pair>

{

public int compare(Pair a, Pair b)

{

if (a.u == b.u) return a.v - b.v;

return a.u - b.u;

}

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int tests = con.nextInt();

while(tests-- > 0)

{

int n = con.nextInt();

int m = con.nextInt();

int p = con.nextInt();

int q = con.nextInt();

mas = new int[n+1];

size = new int[n+1];

for(int i = 1; i <= n; i++)

{

mas[i] = i;

size[i] = 1;

}

Vector<Edge> v = new Vector<Edge>();

for(int i = 0; i < m; i++)

{

int x = con.nextInt();

int y = con.nextInt();

int dist = con.nextInt();

v.add(new Edge(x,y,dist));

}

Collections.sort(v, new MyFun());

TreeSet<Pair> s = new TreeSet<Pair>(new PairFun());

for(int i = 0; i < m; i++)

if (Union(v.get(i).u,v.get(i).v) == 1) s.add(new Pair(v.get(i).u,v.get(i).v));

if(s.contains(new Pair(p,q)) || s.contains(new Pair(q,p)))

System.out.println("YES");

else

System.out.println("NO");

}

con.close();

}

}