6581. Атакующие ладьи

Красивые шахматные задачи являются распространенным источником упражнений в алгоритмах. Начиная с известной задачи о 8 ферзях, было сделано несколько обобщений и вариаций. Одна из них – задача об n ладьях, состоящая в расположении n ладей на шахматной доске размера n на n так, чтобы они не били друг друга.

Профессор Ананд презентовал задачу об n ладьях перед студентами. Так как ладьи бьют друг друга только когда они находятся на одной горизонтали или вертикали, студенты быстро нашли решение, поставив все ладьи на главной диагонали. Профессор решил усложнить задачу, добавив на доску несколько пешек, две ладьи бьют друг друга только если они находятся на одной вертикали или горизонтали, и при этом между ними нет пешек. Поскольку пешки занимают определенные поля, то у ладей появляются ограничения на клетки, куда их можно поставить.

По размеру доски и расположению пешек укажите профессору Ананду максимальное количество ладей, которое можно поставить на пустых клетках так, чтобы они не били друг друга.

Вход. Первая строка содержит число n (1 ≤ n ≤ 100) - количество строк и столбцов на доске. Каждая из следующих n строк содержит n символов. В i-ой строке j-ый символ указывает на содержимое в i-ой строке и j-ой колонке доски. Символом может быть или "." (точка) или буква верхнего регистра "X", указывающие на соответственно пустую клетку или клетку с пешкой.

Выход. Выведите максимальное количество ладей, которое можно поставить на пустых клетках так чтобы они не били друг друга.

Пример входа	Пример выхода
5 X.... X.... ..X.. .X... ....X	7

РЕШЕНИЕ

графы – максимальное паросочетание

Анализ алгоритма

Построим матрицы h горизонтального и v вертикального передвижения ладей. Матрицы содержат нули в тех ячейках, в которых стоят пешки (символы 'X').

Клетки, по которым может двигаться одна ладья в горизонтальном направлении, содержат одинаковые числа. Таким образом, мы получаем набор горизонтальных прямоугольников, каждый из которых содержит в своих ячейках одинаковые числа. То же самое относится и к клеткам для вертикальных движений ладьи.

Далее строим двудольный граф. Каждый горизонтальный прямоугольник имеет некий номер i. Этому прямоугольнику поставим в соответствие i-ую вершину первой доли. Ее следует соединить с теми вершинами второй доли, номера которых совпадают с номерами вертикальных прямоугольников, пересекающих i-ый горизонтальный прямоугольник.

Остается найти величину максимального паросочетания.

Пример

Матрицы горизонтального и вертикального передвижения ладей:

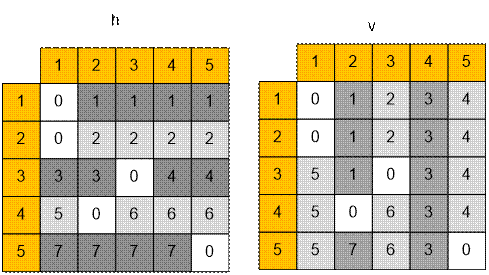
Двудольный граф, максимальное паросочетание и оптимальное расположение ладей:

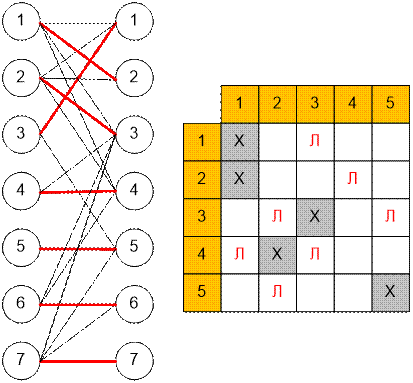
Реализация алгоритма

Объявим используемые массивы.

#define MAX 111

char s[MAX][MAX];

int h[MAX][MAX], v[MAX][MAX];

vector<int> used, par, mt;

vector<int> g[MAX*MAX];

Запускаем поиск в глубину из вершины v. Стараемся найти дополняющий путь, стартующий из v.

int dfs(int v)

{

if (used[v]) return 0;

used[v] = 1;

for (int i = 0; i < g[v].size(); i++)

{

int to = g[v][i];

if (mt[to] == -1 || dfs(mt[to]))

{

mt[to] = v;

par[v] = to;

return 1;

}

}

return 0;

}

Ищем максимальное паросочетание методом дополняющего пути.

void AugmentingPath(void)

{

mt.assign(ver, -1);

par.assign(hor, -1);

for (int run = 1; run; )

{

run = 0; used.assign(hor, 0);

for (int i = 1; i < hor; i++)

if ((par[i] == -1) && dfs(i)) run = 1;

}

}

Основная часть программы. Читаем входные данные.

cin >> n;

s[0] = string(n + 1, ' ');

for (i = 1; i <= n; i++)

{

cin >> s[i];

s[i] = " " + s[i];

}

Строим матрицы h и v – соответственно горизонтальных и вертикальных ходов ладей на имеющейся доске.

hor = ver = 1;

for(i = 1; i <= n; ++i)

for(j = 1; j <= n; ++j)

if(s[i][j] == '.')

{

h[i][j] = (s[i][j - 1] == '.' ? h[i][j - 1] : hor++);

v[i][j] = (s[i - 1][j] == '.' ? v[i - 1][j] : ver++);

Строим двудольный граф.

g[h[i][j]].push_back(v[i][j]);

}

Запускаем поиск максимального паросочетания.

AugmentingPath();

Вычисляем величину максимального паросочетания flow и выводим ее.

flow = 0;

for (i = 1; i < ver; i++)

if (mt[i] != -1) flow++;

cout << flow;