6583. Подсчет единиц

Карл – самый счастливый ребенок в мире: он сегодня утром узнал, что такое двоичная система счисления. Он например узнал, что бинарное представление положительного числа k есть строка a_na_n-1...a₁a₀, где каждое a_i – цифра 0 или 1, начиная с a_n = 1, при этом k = 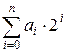. Очень интересно наблюдать превращение десятичных чисел в двоичные, а также складывать и умножать их.

Цезарь – старший брат Карла, и он не может просто так стоять и наблюдать за счастьем брата. Поэтому он приготовил задачу: "Посмотри, Карл, у меня есть к тебе вопрос: Я дам тебе два целых числа a и b, а ты скажешь мне сколько 1-иц в бинарном представлении всех чисел от a до b включительно. Приготовься". Карл согласился принять вызов. Через несколько минут он вернулся со списком двоичных представлений всех чисел от 1 до 100. "Цезарь, я готов". Цезарь улыбнулся и сказал: "Хорошо, я выберу a = 10¹⁵ и b = 10¹⁶. Твой список бесполезен".

Карл не хочет проиграть брату, ему необходимо быстрое решение. Можете ли ему помочь?

Вход. В одной строке расположены два целых числа a и b (1 ≤ a ≤ b ≤ 10¹⁶).

Выход. Вывести общее количество цифр 1 в двоичном представлении всех целых чисел от a до b включительно.

Пример входа	Пример выхода
2 12	21

РЕШЕНИЕ

рекурсия

Анализ алгоритма

Обозначим через f(n) количество единиц в бинарном представлении всех целых чисел от 0 до n. Тогда ответом для интервала [a; b] будет значение f(b) – f(a – 1).

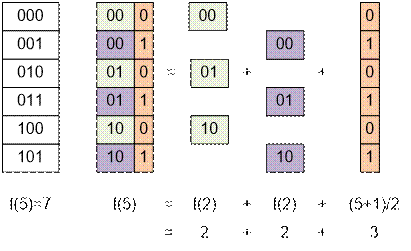
Если n нечетно, то f(n) = 2 * f(n / 2) + .

При четном n положим f(n) = f(n – 1) + s(n), где s(n) – количество единиц в двоичном представлении числа n.

Бзовый случай f(0) = 0.

Пример

Рассмотрим пример, в котором a = 2, b = 12. Ответом для интервала [2; 12] будет значение f(12) – f(1). В единице одна цифра 1 в бинарном представлении, так что f(1) = 1. Вычислим f(12):

f(12) = f(11) + s(12) = f(11) + 2	f(12) = f(11) + 2 = 20 + 2 = 22
f(11) = 2 * f(5) + = 2 * f(5) + 6	f(11) = 2 * f(5) + 6 = 2 * 7 + 6 = 20
f(5) = 2 * f(2) + = 2 * f(2) + 3	f(5) = 2 * f(2) + 3 = 2 * 2 + 3 = 7
f(2) = f(1) + s(2) = 1 + 1 = 2

Ответ равен f(12) – f(1) = 22 – 1 = 21.

Реализация алгоритма

Функция s(n) находит количество единиц в двоичном представлении числа n.

int s(long long n)

{

int cnt = 0;

while(n)

{

cnt += n % 2;

n /= 2;

}

return cnt;

}

Функция f(n) находит количество единиц в бинарном представлении всех целых чисел от 0 до n. Отметим, что = .

long long f(long long n)

{

if (n < 1) return 0;

if (n % 2)

return 2 * f(n / 2) + (n + 1) / 2;

return f(n - 1) + s(n);

}

Основная часть программы. По заданным числам a и b вычисляем и выводим f(b) – f(a – 1).

scanf("%lld %lld",&a,&b);

res = f(b) - f(a - 1);

printf("%lld\n",res);