6583. Counting Ones

Carl is right now the happiest child in the world: he has just learned this morning what the binary system is. He learned, for instance, that the binary representation of a positive integer k is a string a_na_n-1...a₁a₀, where each a_i is a binary digit 0 or 1, starting with a_n = 1 and such that k = . It is really nice to see him turning decimal numbers into binary numbers, and then adding and even multiplying them.

Caesar is Carl's older brother, and he just can't stand to see his little brother so happy. So he has prepared a challenge: "Look Carl, I have an easy question for you: I will give you two integers a and b, and you have to tell me how many 1's there are in the binary representation of all the integers from a to b, inclusive. Get ready". Carl agreed to the challenge. After a few minutes, he came back with a list of the binary representation of all the integers from 1 to 100. "Caesar, I'm ready". Caesar smiled and said: "Well, let me see, I choose a = 10¹⁵ and b = 10¹⁶. Your list will not be useful".

Carl hates loosing to his brother so he needs a better solution fast. Can you help him?

Input. A single line that contains two integers a and b (1 ≤ a ≤ b ≤ 10¹⁶).

Output. Print a line with an integer representing the total number of digits 1 in the binary representation of all the integers from a to b inclusive.

Sample input	Sample output
2 12	21

SOLUTION

recursion

Algorithm analysis

Let f(n) be the number of ones in binary representation of all integers from 0 to n. Then the answer for the interval [a; b] is the value f(b) – f(a – 1).

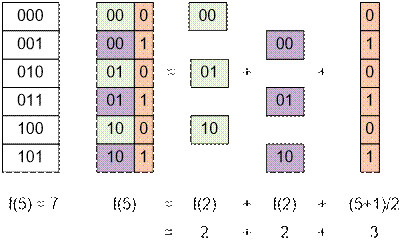
If n is odd, then f(n) = 2 * f(n / 2) + .

If n is even, let f(n) = f(n – 1) + s(n), where s(n) is the number of ones in binary representation of n.

The base case is f(0) = 0.

Example

Consider the sample case, where a = 2, b = 12. The answer for the interval [2; 12] will be the value of f(12) – f(1). There is one digit 1 in binary representation of the number 1, so f(1) = 1. Compute f(12):

f(12) = f(11) + s(12) = f(11) + 2	f(12) = f(11) + 2 = 20 + 2 = 22
f(11) = 2 * f(5) + = 2 * f(5) + 6	f(11) = 2 * f(5) + 6 = 2 * 7 + 6 = 20
f(5) = 2 * f(2) + = 2 * f(2) + 3	f(5) = 2 * f(2) + 3 = 2 * 2 + 3 = 7
f(2) = f(1) + s(2) = 1 + 1 = 2

The answer is f(12) – f(1) = 22 – 1 = 21.

Algorithm realization

Function s(n) finds the number of ones in binary representation of n.

int s(long long n)

{

int cnt = 0;

while(n)

{

cnt += n % 2;

n /= 2;

}

return cnt;

}

Function f(n) finds the number of ones in binary representation of all integers from 0 to n. Note that = .

long long f(long long n)

{

if (n < 1) return 0;

if (n % 2)

return 2 * f(n / 2) + (n + 1) / 2;

return f(n - 1) + s(n);

}

The main part of the program. Read the values a and b, find and print the answer f(b) – f(a – 1).

scanf("%lld %lld",&a,&b);

res = f(b) - f(a - 1);

printf("%lld\n",res);