6613. Дробное зелье

Фредди практикует различные виды альтернативной медицины, такие как гомеопатия. Эта практика основана на убеждении, что последовательно разбавляя некоторые вещества в воде или спирте и тщательно перемешивая их, можно получить лекарства от многих заболеваний.

В этом году овощи Фредди чем-то заболели, и он решил немного поэкспериментировать и исследовать, работает ли гомеопатия также для овощей. Так как Фредди также большой поклонник математики, он не настаивает, чтобы эти вещества имели малые концентрации, однако вместо этого требует, чтобы концентрации имели величины, обратные целым числам (1/n). При выполнении экспериментов некоторым овощам действительно становилось лучше.

Видя успехи Фредди, его сотрудник садовник тоже хочет попробовать один из этих снадобий и просит у него колбу снадобья. У Фреди имеется одна фляга зелья в концентрации 1/n, но он не хочет отдавать ее всю. Вам следует установить, сколькими способами можно разделить зелье на две колбы (разбавив при необходимости) так, чтобы обе результирующие части имели объем, равный объему исходной фляги, а результирующие концентрации были также обратными к целым числам – мы же не хотим в конечном счете получить бесполезную жидкость, не так ли?

Вход. Каждая строка содержит один тест. Строка содержит выражение 1/n (1 ≤ n ≤ 10000), представляя исходную концентрацию.

Выход. Для каждого теста выведите в отдельной строке общее количество различных пар {x, y} натуральных чисел, удовлетворяющих уравнению 1/x + 1/y = 1/n. Пары, отличающиеся порядком следования слагаемых, считаются одинаковыми.

Пример входа	Пример выхода
1/2 1/4 1/1 1/5000	2 3 1 32

РЕШЕНИЕ

теория чисел – количество делителей

Анализ алгоритма

Уравнение 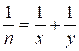эквивалентно ,

,

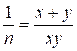Количество пар решений (x, y) равно количеству представления числа n² в виде произведения двух множителей. Оно в свою очередь равно количеству делителей числа n².

Если n = , то количество его делителей равно

d(n) = (a₁ + 1) * (a₂ + 1) * … * (a_k + 1)

Количество делителей числа n² равно

d(n²) = (2a₁ + 1) * (2a₂ + 1) * … * (2a_k + 1)

Для каждого разложения числа n² на два множителя d * (n² / d) получим одну пару решений (x, y):

,

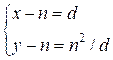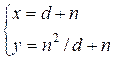
Пары, отличающиеся порядком следования слагаемых, считаются одинаковыми. Различных пар будет в точности d(n²) / 2 + 1.

Пример

Пусть n = 12. Поскольку 12 = 2² * 3 , то d(12²) = (2 * 2 + 1) * (2 * 1 + 1) = 5 * 3 = 15.

Различных пар будет в точности d(n²) / 2 + 1 = 15 / 2 + 1 = 8.

Искомыми парами будут (1, 144), (2, 72), (3, 48), (4, 36), (6, 24), (8, 18), (9, 16), (12, 12).

Реализация алгоритма

Читаем входные данные. Инициализируем текущий ответ задачи res единицей.

while(scanf("%d/%d",&n,&n) == 2)

{

res = 1;

Для каждого простого делителя i числа n подсчитываем степень c, с которой он входит в n. Умножаем результат res на 2c + 1.

for(i = 2; i <= sqrt(n); i++)

{

for(c = 0; n % i == 0; c++) n /= i;

res = res * (2 * c + 1);

}

Если n > 1 по окончанию цикла, то оно равно простому делителю исходного числа n. Этот делитель входит в n со степенью 1, следовательно res необходимо умножить на 2 * 1 + 1 = 3.

if (n > 1) res *= 3;

Выводим результат.

printf("%d\n",res/2 + 1);

}