6828. Bread sorting

 

Michael works in a bakery. At the end of each shift, his boss asks him to sort the loaves of bread in a certain order. However, she cannot decide exactly what that order should be — according to Michael’s observations, it seems to be different every day.

Michael has been working at the bakery for some time and has learned a clever trick with his wooden bread paddle. He can scoop up three adjacent loaves with the paddle and toss them into the air so that when they land, the rightmost loaf moves to the leftmost position, while the other two loaves shift one position to the right. In other words, he can perform a cyclic right rotation on any subsequence of three consecutive loaves.

Before the end of the shift, his colleagues have already placed the bread in one long line. Michael wants to sort the loaves using his paddle trick. He can pick up any three consecutive loaves in the line, rotate them as described, and put them back. However, sometimes it does not matter how many times he uses the paddle — sorting the bread into the order required by his boss may simply be impossible.

 

Input. The first line contains an integer n (3 ≤ n ≤ 105).  Then two lines follow:

·        the first line contains a permutation of the integers from 1 to n, representing the current order of the loaves;

·        the second line contains a permutation of the integers from 1 to n, representing the order of the loaves required by the boss.

 

Output. Print “Possible” if Michael can use his paddle to sort the loaves into the order required by his boss. Otherwise, print “Impossible”.

 

Sample input 1

Sample output 1

4

1 3 4 2

4 3 2 1

Possible

 

 

Sample input 2

Sample output 2

6

1 2 3 4 5 6

6 5 4 3 2 1

Impossible

 

 

SOLUTION

number of invertions

 

Algorithm analysis

The paddle trick performs the following permutation of the loaves:

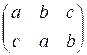
It can be represented as two swaps of adjacent elements:

(a, b, c) → (a, c, b) → (c, a, b)

Each swap of adjacent elements changes the parity of the permutation. Therefore, this operation on the loaves preserves the parity of the permutation.

It is possible to sort the loaves in the order required by Michael’s boss only if the parities of the permutations coincide.

 

A linear solution to the problem is based on the fact that two permutations have the same parity if and only if the parity of the number of cycles in their decompositions is the same.

 

Lemma. Consider the following fact from permutation theory:

parity of a permutation = (n – number of cycles) mod 2

Therefore, to check the parity one can:

·        decompose the permutation into cycles;

·        count the number of cycles.

If two permutations have the same parity of the number of cycles, then their permutation parities coincide.

 

Intuitively, this follows from the fact that each cycle of length k can be constructed from k – 1 swaps of elements; therefore, the total number of swaps is equal to

n – number of cycles

 

Example

In the first example, the first permutation contains 2 inversions, while the second contains 6 inversions. The number of inversions in both permutations has the same parity.

Let us decompose the permutations into cycles:

·        (1, 3, 4, 2) = (1) (3, 4, 2);

·        (4, 3, 2, 1) = (4, 1) (3, 2);

Both permutations consist of two cycles; therefore, the number of cycles in them also has the same parity.

 

In the second example, the first permutation contains 0 inversions, while the second contains 15 inversions. The number of inversions in these permutations has different parity.

Let us decompose the permutations into cycles:

·        (1, 2, 3, 4, 5, 6) = (1) (2) (3) (4) (5) (6);

·        (6, 5, 4, 3, 2, 1) = (6, 1) (5, 2) (4, 3);

The first permutation consists of 6 cycles, while the second consists of 3 cycles. Thus, the parity of the number of cycles in these permutations is different.

 

Algorithm implementation

Compute the number of inversions in both permutations in O(nlog2n) and compare their parity.

 

#include <cstdio>

#include <string>

#include <vector>

#define MAX 100010

using namespace std;

 

int m[MAX];

int n, i, j;

long long swaps, sw;

 

void merge(int *a, int bleft, int bright, int cleft, int cright)

{

  // a[bleft..bright] -> res[]

  // res[0..len-1] a[cleft..cright] are merged into a[bleft..cright]

  // we copy only half of array

  int i, len = bright - bleft + 1, resCur = 0;

  int *res = new int[len];

  memcpy(res,a + bleft,len*sizeof(int));

  while((resCur < len) && (cleft <= cright))

  {

    if (res[resCur] <= a[cleft]) a[bleft++] = res[resCur++];

    else a[bleft++] = a[cleft++], swaps += len - resCur;

  }

  while (resCur < len) a[bleft++] = res[resCur++];

  delete[] res;

}

 

void mergeSort(int *a, int left, int right)

{ 

  if (left >= right) return;

  int middle = (left + right) / 2;

  mergeSort(a,left,middle);

  mergeSort(a,middle+1,right);

  merge(a, left, middle, middle + 1, right);

}

 

int main(void)

{

  scanf("%d",&n);

  for(swaps = i = 0; i < n; i++) scanf("%d",&m[i]);

  mergeSort(m, 0, n - 1); sw = swaps % 2;

 

  for(swaps = i = 0; i < n; i++) scanf("%d",&m[i]);

  mergeSort(m, 0, n - 1); swaps %= 2;

 

  if (sw == swaps) printf("Possible\n");

  else printf("Impossible\n");

  return 0;

}

 

Algorithm implementation – number of cycles in permutation

Declare an array to store the permutation.

 

#define MAX 100010

int a[MAX];

 

The function run traverses one cycle of the permutation starting from index pos. At each step, it moves to the next element of the cycle according to the rule pos → a[pos]. Visited elements are marked with the value -1 to avoid processing them again. Thus, the function completely traverses one cycle of the permutation and marks all its elements as already visited.

 

void run(int pos)

{

  int v;

  while (a[pos] != -1)

  {

    v = a[pos];

    a[pos] = -1;

    pos = v;

  }

}

 

The function parity computes the parity of the number of cycles in the permutation a, that is, it returns the number of cycles modulo 2. The function sequentially scans all positions of the array.

 

int parity(int *a)

{

  int res = 0;

 

Sequentially examine all positions of the array.

 

  for (int i = 0; i < n; i++)

 

If an element has not yet been visited (a[i] ≠ -1), this means the beginning of a new cycle. In this case, the function run(i) is called, which traverses the entire cycle and marks its elements with the value -1.

 

    if (a[i] != -1)

    {

      run(i);

 

After traversing the cycle, the counter res is increased by 1.

 

      res++;

    }

 

Return the parity of the number of cycles.

 

  return res % 2;

}

 

The main part of the program. Read the first permutation. During input, each value is decreased by 1 (a[i]--) to convert from 1-based indexing (1..n) to the more convenient 0-based indexing (0 .. n – 1).

 

scanf("%d",&n);

for (i = 0; i < n; i++)

  scanf("%d",&a[i]), a[i]--;

 

In the variable p1, compute the parity of the number of cycles in the permutation a.

 

p1 = parity(a);

 

Read the second permutation. In the variable p2, compute the parity of the number of cycles in the permutation a.

 

for (i = 0; i < n; i++)

  scanf("%d",&a[i]), a[i]--;

p2 = parity(a);

 

Compare the parities of the number of cycles in the two permutations and print the result.

 

if (p1 == p2) printf("Possible\n");

else printf("Impossible\n");