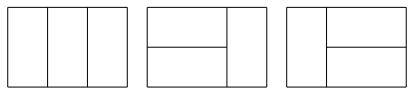
628. Доминошки

Дана прямоугольная доска m × n. Найдите количество способов замостить её доминошками – прямоугольниками размера 1 × 2 клетки.

Вход. Два числа m и n (1 ≤ m, n ≤ 10).

Выход. Выведите количество способов, которыми можно замостить доску заданного размера доминошками.

Пример входа	Пример выхода
2 3	3

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Пусть прямоугольная доска имеет m строк и n колонок.

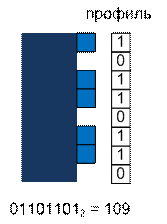
Профилем будем называть столбец. Хранить его будем в виде двоичной маски. В качестве состояния динамики будем использовать профили размера m. В этом профиле 1 означает, что домино лежит горизонтально и заканчивается на этом столбце, иначе 0. Таких профилей будет 2^m.

Пусть d[i][j] = 1, если из профиля i можно перейти в j-ый, иначе d[i][j] = 0.

Пусть a[i][p₁] – количество способов замощения первых i – 1 столбцов и заканчивающийся на профиле p₁. Тогда

a[i][p₁] =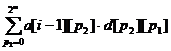

Ответом будет a[n + 1][0].

Реализация алгоритма

Объявим рабочие массивы:

· d – таблица переходов: d[i][j] = 1, если из профиля i можно перейти в профиль j. Иначе d[i][j] = 0.

· a – результирующая матрица: a[i][p₁] равно количеству замощения первых i – 1 столбцов, заканчивающихся профилем p₁.

#define MAX 10

int d[1<<MAX][1<<MAX];

long long a[MAX+2][1<<MAX];

Возвращает значение pos-бита в числе x.

int bit(int x, int pos)

{

if (pos < 0) return 0;

return (x & (1 << pos));

}

Генерирует все профили p₂, в которые можно попасть из p₁. Далее устанавливаем d[p₁][p₂] = 1.

void go(int p1, int p2, int pos)

{

Профиль p₁ просмотрен до конца, до m-ой позиции. Значит из p₁ можно получить p₂.

if (pos == m)

{

d[p1][p2] = 1;

return;

}

Если ячейка (бит) pos в профиле p₁ не занятый.

if (bit(p1,pos) == 0)

{

Тогда кладем горизонтальное домино.

go(p1,p2 + (1LL << pos), pos+1);

Если не занята и следующая, (pos + 1)-ая ячейка, то ложим вертикальную доминошку. При этом в профиль p₂ ничего не добавляем, увеличиваем pos на 2.

if (pos < m - 1)

if (bit(p1,pos+1) == 0) go(p1,p2,pos+2);

}

else

Ячейка pos в профиле p₁ занята, увеличиваем на 1 позицию pos в профиле p₁.

go(p1,p2,pos+1);

}

Основная часть программы. Читаем входные данные.

scanf("%d %d",&m,&n);

memset(d,0,sizeof(d));

memset(a,0,sizeof(a));

Заполнение таблица переходов d. Для каждого профиля i находим все профили, в которые можно перейти.

for(i = 0; i < (1 << m); i++)

go(i,0,0);

Пересчитываем результирующую матрицу.

a[1][0] = 1;

for(i = 2; i <= n + 1; i++)

for(p1 = 0; p1 < (1 << m); p1++)

{

a[i][p1] = 0;

for(p2 = 0; p2 < (1 << m); p2++)

a[i][p1] += a[i-1][p2] * d[p2][p1];

}

Выводим ответ.

printf("%lld\n",a[n+1][0]);