666. Triangle and point

The triangle and the point are given on the 2D coordinate plane. Is the point In, On or Out of the triangle?

Input. The coordinates of the vertices of a triangle are given in the first 3 lines (each line contains 2 integers). The fourth line contains the point’s coordinates in the same format. All numbers are integers; their absolute values are no more than 10000. The vertices of triangle do not lie on a straight line.

Output. Print the word “In” if the point is located inside the triangle, “On” if the point lies on the border of triangle (on the vertex or on the edge), and “Out” if the point is outside the triangle.

Пример входа	Пример выхода
-2 -2 3 1 0 1 0 0	In

SOLUTION

geometry

Algorithm analysis

Point O lies inside triangle ABC if and only if all three turns OAB, OBC and OCA are right (triangle ABC is oriented clockwise) or left (triangle ABC is oriented counterclockwise). That is, if all expressions OA ´ AB, OB ´ BC, OC ´ CA have the same sign (here ´ denotes the cross product).

Let a(x₁, y₁) and b(x₂, y₂) be the coordinates of the vectors. Then

a ´ b = 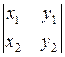= x₁y₂ – x₂y₁

Point O lies on the border of the triangle if all expressions OA ´ AB, OB ´ BC, OC ´ CA are either non-negative or non-positive, but one of them is necessarily equal to 0. For example, if O lies on the side BC, then OB ´ BC = 0.

Algorithm realization

Read the coordinates of the vertices of triangle A, B, C and point O. Compute the required cross products.

scanf("%d %d %d %d %d %d %d %d",&xA,&yA,&xB,&yB,&xC,&yC,&xO,&yO);

// OA = (xA - xO,yA - yO)

// AB = (xB - xA,yB - yA)

OAxAB = (xA - xO)*(yB - yA) - (xB - xA)*(yA - yO);

// OB = (xB - xO,yB - yO)

// BC = (xC - xB,yC - yB)

OBxBC = (xB - xO)*(yC - yB) - (xC - xB)*(yB - yO);

// OC = (xC - xO,yC - yO)

// CA = (xA - xC,yA - yC)

OCxCA = (xC - xO)*(yA - yC) - (xA - xC)*(yC - yO);

If all computed products are of the same sign, then point O lies inside the triangle ABC. If one of the products is equal to zero, point O lies on the border of the triangle. Otherwise, point O is outside the triangle.

if (((OAxAB > 0) && (OBxBC > 0) && (OCxCA > 0)) ||

((OAxAB < 0) && (OBxBC < 0) && (OCxCA < 0))) printf("In\n");

else

if (((OAxAB >= 0) && (OBxBC >= 0) && (OCxCA >= 0)) ||

((OAxAB <= 0) && (OBxBC <= 0) && (OCxCA <= 0))) printf("On\n");

else printf("Out\n");