682. Sum on a segment

Given array of integers a₁, ..., a_n. For given indexes l and r find

Input. The first line contains the amount of numbers n (1 ≤ n ≤ 10⁶). The second line contains the numbers a_i (1 ≤ a_i ≤ 1000) space separated. The third line contains the number of queries m (1 ≤ m ≤ 10⁶). Each of the next line contains the query l_i and r_i (1 ≤ l_i ≤ r_i ≤ n).

Output. Print in separate m lines the numbers S_li..ri.

Sample input	Sample output
5 1 2 3 4 5 5 1 5 2 3 3 4 2 5 1 4	15 5 7 14 10

SOLUTION

partial sums

Algorithm analysis

Each query S_l,r can be performed using a loop with a complexity of O(n). We have m ≤ 10⁶ queries and the length of the array is n ≤ 10⁶. If each query runs in linear time, we would need no more than n * m ≤ 10¹² operations, which will exceed the Time Limit.

Consider the partial sums of array а:

s₁ = a₁;

s₂ = a₁ + a₂;

s₃ = a₁ + a₂ + a₃;

. . .

s_n = a₁ + a₂ + a₃ + . . . + a_n;

It is possible to compute the values s₁, s₂, …, s_n in a linear array s in O(n) time.

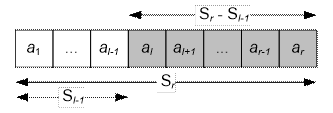
Further note that

S_l,r = a_l + a_{l + 1} + … + a_r =

= (a₁ + … + a_l + a_{l + 1} + … + a_r) – (a₁ + … + a_l-1) = s_r – s_l-1

So we can answer the query S_l,r in constant time.

Example

Let’s compute the sum a₃ + a₄ + a₅ for the input example.

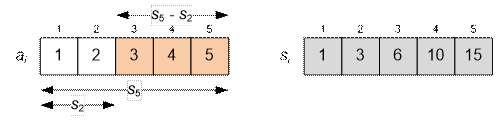
We have: a₃ + a₄ + a₅ = s₅ – s₂ = 15 – 3 = 12.

Algorithm realization

Declare two working two-dimensional arrays.

#define MAX 1000001

int a[MAX], s[MAX];

Read the input set of numbers into array a, and calculate the partial sums in array s.

scanf("%d",&n); s[0] = 0;

for(i = 1; i <= n; i++)

{

scanf("%d",&a[i]);

s[i] = s[i-1] + a[i];

}

Process m queries.

scanf("%d",&m);

for(i = 0; i < m; i++)

{

scanf("%d %d",&b,&c);

printf("%d\n",s[c] - s[b-1]);

}

Python realization

Read the input data.

n = int(input())

a = [0] + list(map(int, input().split()))

Calculate the partial sums of list a in list s.

s = [0] * (n + 1)

for i in range(1, n + 1):

s[i] = s[i - 1] + a[i]

Process m queries.

m = int(input())

for _ in range(m):

b, c = map(int, input().split())

print(s[c] - s[b - 1])