691. Разреженные таблицы
Дан массив из n чисел. Требуется написать программу,
которая будет отвечать на запросы следующего вида: найти минимум на отрезке
между u и v включительно.
Вход. В первой строке
входного файла даны три натуральных числа n,
m (1 ≤ n ≤ 105, m
≤ 107) и a1
(1 ≤ a1 <
16714589) – количество элементов в массиве, количество запросов и первый
элемент массива соответственно. Вторая строка содержит два натуральных числа u1 и v1 (1 ≤ u1,
v1 ≤ n) – первый запрос.
Элементы a2,
a3, ..., an заданы следующей формулой:
ai+1 = (23·ai + 21563) mod 16714589.
Например, при n =
10, a1 = 12345 получается
следующий массив:
a = (12345, 305498, 7048017, 11694653,
1565158, 2591019, 9471233, 570265, 13137658, 1325095)
Запросы генерируются следующим образом:
ui+1 = ((17·ui + 751 + ansi + 2i) mod n) + 1,
vi+1 = ((13·vi + 593 + ansi + 5i) mod n) +1,
где ansi
– ответ на запрос номер i.
Выход. Вывести um,
vm и ansm (последний запрос и ответ на него).
|
Пример
входа |
Пример
выхода |
|
10 8 12345 3 9 |
5 3 1565158 |
РЕШЕНИЕ
структуры
данных - RMQ
Анализ алгоритма
Задача решается
с использованием статической структуры данных Range Minimum Query (RMQ).
Для каждого i (1 £ i £ n) и j (1 £ j £ log2n) в ячейке m[i][j] будем хранить
индекс наименьшего элемента на промежутке (i,
…, i + 2j – 1), то есть m[i][j] хранит информацию об индексе
минимального элемента в блоке длины 2j,
начинающегося с позиции i. Разобьем
промежуток (i, …, i + 2j
– 1) на два равных: (i, …, i + 2j-1
– 1) и (i + 2j-1, …, i
+ 2j – 1). Тогда m[i][j]
равно индексу меньшего элемента среди a[m[i][j
– 1]] и a[m[i + 2j-1][j – 1]]. Рекуррентное уравнение для
вычисления m[i][j] имеет вид:
m[i][j]
=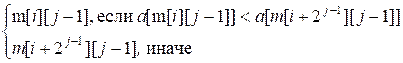
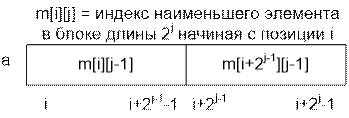
Инициализация:
m[i][0] = i
Для заданных
индексов i и j требуется найти индекс с наименьшим элементом (Range Minimum
Query) в подмассиве A[i…j]. Такой запрос будем обозначать RMQA(i, j).
Для выполнения
запроса RMQA(i, j) следует разбить интервал (i, j)
на два пересекающихся интервала с длинами, являющимися степенями двойки, и
найти минимум среди их наименьших значений. Выберем, например, k = log2(j – i). Тогда двумя
интервалами, покрывающими (i, j), будут (i, …, i + 2k – 1) и (j – 2k
+ 1, …, j). Откуда RMQA(i, j)
равно индексу меньшего элемента среди a[m[i][k]]
и a[m[j – 2k + 1][k]].
Время
предварительной обработки массива m и построения массива а равно O(nlogn), а время
выполнения запроса RMQA(i,
j) константно и составляет O(1).
Реализация алгоритма
Входную
последовательность ai
длины n ≤ 105 храним
в массиве а. Объявим массив mas для выполнения предобработки данных.
#define MAX 100001
#define LOGMAX 17
int a[MAX];
int mas[MAX][LOGMAX];
Если u > v, то функция check меняет их
местами.
void check(int
&u, int &v)
{
int temp;
if (u > v)
temp = u, u = v, v = temp;
}
Функция RMQ_nlogn заполняет массив m описанным выше образом.
void RMQ_nlogn(void)
{
int i, j;
for (i = 1; i
<= n; i++) mas[i][0] = i;
for (j = 1;
(1 << j) <= n; j++)
for (i = 1;
i + (1 << j) - 1 <= n; i++)
if
(a[mas[i][j - 1]] < a[mas[i + (1 << (j - 1))][j - 1]])
mas[i][j] = mas[i][j - 1];
else
mas[i][j] = mas[i + (1 << (j - 1))][j - 1];
}
Функция q совершает запрос RMQA(i, j)
и возвращает индекс с наименьшим элементом (Range Minimum Query) в подмассиве a[i…j].
int q(int
i, int j)
{
int k = (int)(log(1.0*j - i + 1) / log(2.0));
int res =
mas[i][k];
if (a[mas[j -
(1<<k) + 1][k]] < a[res])
res = mas[j -
(1<<k) + 1][k];
return res;
}
Основная часть программы. Читаем
входные данные.
scanf("%d %d",&n,&m);
scanf("%d %d %d",&a[1],&u,&v);
Генерируем массив a2,
a3, ..., an.
for(i = 2; i <= n; i++)
a[i] = (23 * a[i-1] + 21563) % 16714589;
Строим массив m, в котором m[i][j]
хранит индекс наименьшего элемента на промежутке (i, …, i + 2j – 1). То есть m[i][j]
содержит индекс минимального элемента в блоке длины 2j, начинающегося с позиции i.
RMQ_nlogn();
for(i = 1; i <= m; i++)
{
Если в запросе u > v, то меняем их
местами функцией check.
u1 = u; v1 = v; check(u1,v1);
Запрос q(u1,v1)
возвращает индекс наименьшего элемента на отрезке a[u1] … a[v1].
ans = a[q(u1,v1)];
if (i < m)
{
Генерируем данные для следующего
запроса.
u = ((17*u + 751 + ans + 2*i) % n) + 1;
v = ((13*v + 593 + ans + 5*i) % n) + 1;
}
}
Выводим ответ.
printf("%d %d %d\n",u,v,ans);