694. Минимум в очереди
На вход
программы подается набор операций с очередью. Каждая операция состоит в
добавлении или удаления элемента из очереди. После выполнения каждой операции
найдите наименьшее число, которое находится в очереди. Сложите все полученные
числа и получите ответ. Если после некоторой операции очередь оказалась пуста,
то ничего не прибавляйте к ответу. Если выполнить удаление невозможно, так как
очередь пуста, то не выполняйте его.
Вход. Входные данные генерируются в самой программе. На вход
подаются параметры для генерации входной последовательности.
Первое число n (1
≤ n ≤ 106) содержит
количество операций с очередью. Затем идут четыре неотрицательных числа a, b,
c, x0, не превосходящие 10000.
Для получения входных данных сгенерируем последовательность x.
Первое число в генерируемой последовательности x1. Первое, а также каждое
следующее число вычисляется из предыдущего по формуле:
xi = (a·![]() + b·xi-1 + c) / 100 mod 106,
+ b·xi-1 + c) / 100 mod 106,
где '/' – операция целочисленного деления, а 'mod' – остаток
от деления.
Если xi
mod 5 < 2, то необходимо удалить число из очереди. В противном случае нужно
добавить в очередь число xi.
Выход. Выведите
искомую сумму.
|
Пример
входа 1 |
Пример
выхода 1 |
|
2 0 0 1 81 |
0 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
3 1 1 1 13 |
0 |
РЕШЕНИЕ
структуры данных - очередь
Анализ алгоритма
В задаче следует
промоделировать работу очереди value. Однако для
того чтобы за O(1) отвечать на вопрос о минимальном элементе в очереди, заведем
еще и очередь минимальных элементов mn. При поступлении
или удалении элемента работу очереди value моделируем
обыкновенным образом. Опишем работу очереди mn:
·
При поступлении элемента x будем удалять из хвоста очереди mn
элементы до тех пор, пока они будут больше x. Затем заносим x в хвост mn.
·
При удалении элемента будем удалять голову очереди mn лишь в том случае, если она совпадает с удаляемым
элементом.
При такой работе с очередью mn текущий наименьший элемент
очереди value будет всегда находиться в голове очереди mn. А элементы очереди
mn будут всегда отсортированы по возрастанию.
Если при решении
задачи использовать структуру данных deque из
стандартной библиотеки шаблонов, то можно получить Time Limit. Следует
промоделировать работу обоих очередей через статические (n ≤ 106) или
динамические массивы.
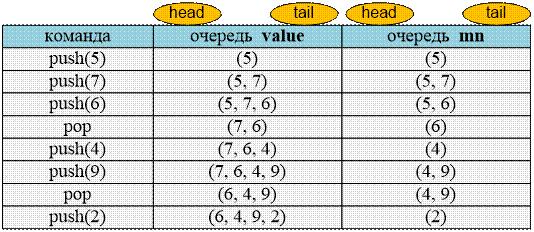
Пример
Промоделируем
работу очередей, например, на следующих командах. Вставка элемента происходит в
конец очереди, а удаление из головы.
Реализация алгоритма
Очередь value будет содержать поступающие на вход числа. Объявим также
очередь минимальных элементов mn.
deque<int>
value, mn;
Читаем входные данные.
scanf("%d %d %d %d %d",&n,&a,&b,&c,&x);
for(i = 1; i <= n; i ++)
{
x = ((1LL * a * x * x + 1LL * b * x + c) /
100) % 1000000LL;
if (x % 5
< 2) // удалить из очереди
{
Удаление элемента из очереди. Если
она пуста, то ничего не делаем. Иначе если голова очереди совпадает с головой
очереди mn (на текущий момент как раз голова очереди value являлась наименьшим
элементом очереди, и при ее удалении минимальный элемент очереди изменится), то
удаляем обе головы.
if
(!value.empty())
{
if
(value.front() == mn.front()) mn.pop_front();
value.pop_front();
}
} else {
Добавляем элемент x в очередь. Удаляем из хвоста очереди
mn элементы, большие x. После чего
заносим x в хвост очереди mn.
value.push_back(x);
while(!mn.empty()
&& (x < mn.back())) mn.pop_back();
mn.push_back(x);
}
Если очередь не пуста, то ее
наименьший элемент находится в голове очереди mn.
if
(!mn.empty()) Res += mn.front();
}
Выводим результат – сумму всех
минимальных элементов.
printf("%lld\n",Res);
Реализация класса с STL
#include <cstdio>
#include <deque>
using namespace
std;
int x, i, n, a, b, c;
long long
Res = 0;
class Deque
{
private:
deque<int>
q, min;
public:
void pop(void)
{
if (!q.empty())
{
if
(q.front() == min.front()) min.pop_front();
q.pop_front();
}
}
int getMin(void)
{
return
(min.empty()) ? 0 : min.front();
}
void push(int x)
{
q.push_back(x);
while(!min.empty()
&& x < min.back()) min.pop_back();
min.push_back(x);
}
};
int main(void)
{
scanf("%d %d
%d %d %d",&n,&a,&b,&c,&x);
Deque d;
for(i = 1; i
<= n; i ++)
{
x = ((1LL * a * x * x + 1LL * b * x + c) /
100) % 1000000LL;
if (x % 5
< 2)
d.pop(); //
удалить из очереди
else
d.push(x); //
добавить в очередь значение x
Res += d.getMin();
}
printf("%lld\n",Res);
return 0;
}
Реализация очереди на массивах
Программа
работает в несколько раз быстрее при реализации очереди на массивах, нежели с
использованием класса deque из STL.
Объявим рабочие
очереди value и mn. Переменные Bvalue и Evalue – указатели на начало и конец очереди value. Переменные Bmn и Emn – указатели на
начало и конец очереди mn. Результат накапливаем в переменной Res. Количество операций с очередью не более 106, поэтому
достаточно использовать массивы такого размера.
#define MAX 1000010
int value[MAX], mn[MAX];
int Bvalue, Evalue, Bmn, Emn;
long long
Res = 0;
Основная часть программы. Читаем
входные данные. Инициализируем указатели начала и конца очередей.
scanf("%d %d %d %d %d",&n,&a,&b,&c,&x);
Bvalue = Evalue
= Bmn = Emn = 0;
for(i = 1; i <= n; i ++)
{
x = ((1LL * a * x * x + 1LL * b * x + c) /
100) % 1000000LL;
if (x % 5
< 2) // удалить из очереди
{
if (Bvalue
!= Evalue)
{
if
(value[Bvalue] == mn[Bmn]) Bmn++;
Bvalue++;
}
} else // добавить в очередь значение x
{
value[Evalue++] = x;
while((Bmn
!= Emn) && (x < mn[Emn-1])) Emn--;
mn[Emn++] = x;
}
if (Bmn !=
Emn) Res += mn[Bmn];
}
printf("%lld\n",Res);
Реализация при помощи класса
#include <stdio.h>
int x, i, n, a, b, c;
long long
Res = 0;
class Deque
{
public:
int *value,
*mn;
int Bvalue,
Evalue, Bmn, Emn;
Deque(int n =
1000010)
{
value = new
int[n];
mn = new int[n];
Bvalue = Evalue = Bmn = Emn = 0;
}
~Deque()
{
delete[]
value;
delete[]
mn;
}
void pop(void)
{
if (Bvalue
!= Evalue)
{
if
(value[Bvalue] == mn[Bmn]) Bmn++;
Bvalue++;
}
}
int getMin(void)
{
return (Bmn
!= Emn) ? mn[Bmn] : 0;
}
void push(int x)
{
value[Evalue++] = x;
while((Bmn
!= Emn) && (x < mn[Emn-1])) Emn--;
mn[Emn++] = x;
}
};
int main(void)
{
scanf("%d %d %d %d %d",&n,&a,&b,&c,&x);
Deque d(n);
for(i = 1; i
<= n; i ++)
{
x = ((1LL * a * x * x + 1LL * b * x + c) /
100) % 1000000LL;
if (x % 5
< 2)
d.pop(); //
удалить из очереди
else
d.push(x); //
добавить в очередь значение x
Res += d.getMin();
}
printf("%lld\n",Res);
return 0;
}
Реализация очереди на основе связанного списка
Реализация
очереди на указателях выгодна тем, что в каждый момент времени памяти тратится
ровно столько, сколько элементов хранится в очереди.
#include <stdio.h>
class deque
{
private:
struct node
{
int data;
node *next, *prev;
node()
{
prev = next = NULL;
}
node(int a)
{
data = a;
prev = next = NULL;
}
} *Head, *Tail;
public:
deque()
{
Head = Tail = NULL;
}
void
push_back(int a)
{
node *p = new
node(a);
if(Head ==
NULL)
Head = Tail = p;
else
{
p->prev = Tail;
p->next = NULL;
Tail->next = p;
Tail = p;
}
}
void
push_front(int a)
{
node *p = new
node(a);
if(Head ==
NULL)
Head = Tail = p;
else
{
p->next = Head;
p->prev = NULL;
Head->prev = p;
Head = p;
}
}
int
pop_front(void)
{
node *p = Head;
int r =
Head->data;
if(Head ==
Tail)
Head = Tail = NULL;
else
{
Head = Head->next;
Head->prev = NULL;
}
delete p;
return r;
}
int pop_back(void)
{
node *p = Tail;
int r =
Tail->data;
if(Head ==
Tail)
Head = Tail = NULL;
else
{
Tail = Tail->prev;
Tail->next = NULL;
}
delete p;
return r;
}
int empty(void)
{
return Head
== NULL;
}
int front(void)
{
return
Head->data;
}
int back(void)
{
return
Tail->data;
}
};
deque value, mn;
int x, i, n, a, b, c;
long long
Res = 0;
int main(void)
{
scanf("%d %d
%d %d %d",&n,&a,&b,&c,&x);
for(i = 1; i
<= n; i ++)
{
x = ((1LL * a * x * x + 1LL * b * x + c) /
100) % 1000000LL;
if (x % 5
< 2) // удалить из очереди
{
if
(!value.empty())
{
if
(value.front() == mn.front()) mn.pop_front();
value.pop_front();
}
} else // добавить в очередь значение x
{
value.push_back(x);
while(!mn.empty()
&& (x < mn.back())) mn.pop_back();
mn.push_back(x);
}
if
(!mn.empty()) Res += mn.front();
}
printf("%lld\n",Res);
return 0;
}
Java реализация
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
LinkedList<Long> value = new LinkedList<Long>();
LinkedList<Long> mn = new LinkedList<Long>();
long n = con.nextLong(), a = con.nextLong();
long b = con.nextLong(), c = con.nextLong();
long x = con.nextLong(), Res = 0;
for(long i = 1; i <= n; i ++)
{
x = ((a * x * x + b * x + c) / 100) %
1000000;
if (x % 5 < 2)
{
if (value.isEmpty() == false)
{
if (value.getFirst().equals(mn.getFirst())) mn.removeFirst();
value.removeFirst();
}
} else
{
value.addLast(x);
while(!mn.isEmpty() && (x < mn.getLast()))
mn.removeLast();
mn.addLast(x);
}
if (!mn.isEmpty()) Res += mn.getFirst();
}
System.out.println(Res);
}
}