694. Minimum
in the Queue
The input to a program is
a set of operations with the queue. Each operation is either addition or
removal of an item to or from the queue. After each operation find the smallest
among all the numbers in a queue. Add up all the resulting numbers and get an
answer. If after any operation the queue is empty, then add nothing to the
answer. If it is impossible to remove an item because the queue is empty,
then do nothing.
Input. The input data will be generated in your program. You will
be given some parameters to get the input sequence.
The first input number n (1 ≤ n ≤ 106) is the number of operations with the
queue. Then four nonnegative integers a,
b, c, x0 are
given. Their values are not greater than 10000.
Let's generate the input
sequence x.
The first number of input
sequence is x1. The first
and each next number can be evaluated from the previous number using the
formula:
xi = (a·![]() + b·xi-1 + c) / 100 mod 106,
+ b·xi-1 + c) / 100 mod 106,
where '/' is an
integer division, 'mod' is the remainder from division.
If xi mod 5 < 2, you must delete the number from the
queue, otherwise add number xi
to the queue.
Output. Print the resulting sum.
|
Sample
input 1 |
Sample
output 1 |
|
2 0 0 1 81 |
0 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
3 1 1 1 13 |
0 |
SOLUTION
data structures - queue
Algorithm analysis
In
the problem you need to simulate the queue value. To answer
the question about the minimum element in the queue in O(1), declare the queue
of minimum elements mn. When element enqueues or dequeues, simulate the queue value in the common manner. Below we describe how the queue mn works:
·
When the element x enqueues, we shall delete from the mn tail the elements until they are greater than x. Then enqueue x into the tail of mn.
·
When the element dequeues, we shall
delete the head from the queue mn only if it equals to the removed element.
During such simulation with queue mn the current minimum element of the queue value will usually be located at the head of the queue mn. And the elements of the queue mn will usually keep the sorted order.
If
one use the data structure deque from
standart template library, it is possible to get Time Limit. Simulate the work
of both queues using static arrays.
Example
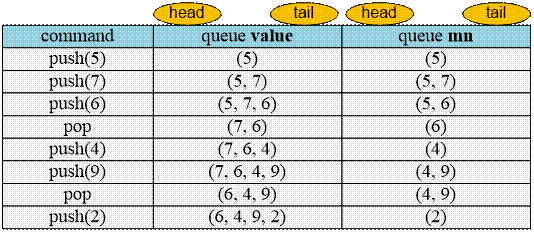
Lets
simulate two queues using the next commands. We insert element to the end of
the queue and remove from the head.
Algorithm realization
The
queue value will contain the input numbers.
deque<int>
value, mn;
Read the input data.
scanf("%d %d %d %d %d",&n,&a,&b,&c,&x);
for(i =
1; i <= n; i ++)
{
x = ((1LL * a * x * x + 1LL * b * x + c) /
100) % 1000000LL;
if (x % 5
< 2) // remove from the queue
{
Remove the element from the
queue. If the queue is empty, do nothing. If the head of the queue coinsides
with the head of the queue mn (it is the case when the head of
queue value is a minimum element in the queue, so after its removing
the minimum element in the queue changes), delete both heads.
if
(!value.empty())
{
if
(value.front() == mn.front()) mn.pop_front();
value.pop_front();
}
} else {
Enqueue the element x. Delete from the tail of the queue mn
the elements greater than x. Then add
x into the tail of queue mn.
value.push_back(x);
while(!mn.empty()
&& (x < mn.back())) mn.pop_back();
mn.push_back(x);
}
If the queue is not empty, its
mimimum element is in the head of the queue mn.
if
(!mn.empty()) Res += mn.front();
}
Print the result – the sum of
all minimum elements.
printf("%lld\n",Res);
Algorithm realization – class with
STL
#include <cstdio>
#include <deque>
using namespace std;
int x, i, n, a, b, c;
long long Res = 0;
class Deque
{
private:
deque<int>
q, min;
public:
void pop(void)
{
if
(!q.empty())
{
if
(q.front() == min.front()) min.pop_front();
q.pop_front();
}
}
int getMin(void)
{
return
(min.empty()) ? 0 : min.front();
}
void push(int x)
{
q.push_back(x);
while(!min.empty()
&& x < min.back()) min.pop_back();
min.push_back(x);
}
};
int main(void)
{
scanf("%d %d
%d %d %d",&n,&a,&b,&c,&x);
Deque d;
for(i = 1; i
<= n; i ++)
{
x = ((1LL * a * x * x + 1LL * b * x + c) /
100) % 1000000LL;
if (x % 5
< 2)
d.pop(); // remove
from the deque
else
d.push(x); // add
value x into the deque
Res += d.getMin();
}
printf("%lld\n",Res);
return 0;
}
Algorithm realization – arrays
The
program works faster when queue is implementated on arrays rather than using
class deque of STL.
Declare
the deques value and mn. Variables Bvalue and Evalue are the
pointers to the start and to the end of deque value. Variables
Bmn and Emn are the
pointers to the start and to the end of deque mn. The result is calculated in the variable Res. The number of operations with deque is no more than 106,
so we can use arrays of this size.
#define MAX
1000010
int
value[MAX], mn[MAX];
int
Bvalue, Evalue, Bmn, Emn;
long long Res = 0;
Main part of the program. Read
the input data. Initialize the pointers to the start and to the end of the
deques.
scanf("%d %d %d %d %d",&n,&a,&b,&c,&x);
Bvalue
= Evalue = Bmn = Emn = 0;
for(i =
1; i <= n; i ++)
{
x = ((1LL * a * x * x + 1LL * b * x + c) /
100) % 1000000LL;
if (x % 5
< 2) // remove from the deque
{
if (Bvalue
!= Evalue)
{
if
(value[Bvalue] == mn[Bmn]) Bmn++;
Bvalue++;
}
} else // add x into the deque
{
value[Evalue++] = x;
while((Bmn
!= Emn) && (x < mn[Emn-1])) Emn--;
mn[Emn++] = x;
}
if (Bmn !=
Emn) Res += mn[Bmn];
}
printf("%lld\n",Res);
Algorithm realization - class
#include <stdio.h>
int x, i, n, a, b, c;
long long Res = 0;
class Deque
{
public:
int *value,
*mn;
int Bvalue,
Evalue, Bmn, Emn;
Deque(int n =
1000010)
{
value = new
int[n];
mn = new int[n];
Bvalue = Evalue = Bmn = Emn = 0;
}
~Deque()
{
delete[]
value;
delete[]
mn;
}
void pop(void)
{
if (Bvalue
!= Evalue)
{
if
(value[Bvalue] == mn[Bmn]) Bmn++;
Bvalue++;
}
}
int getMin(void)
{
return (Bmn
!= Emn) ? mn[Bmn] : 0;
}
void push(int x)
{
value[Evalue++] = x;
while((Bmn
!= Emn) && (x < mn[Emn-1])) Emn--;
mn[Emn++] = x;
}
};
int main(void)
{
scanf("%d %d
%d %d %d",&n,&a,&b,&c,&x);
Deque d(n);
for(i = 1; i
<= n; i ++)
{
x = ((1LL * a * x * x + 1LL * b * x + c) /
100) % 1000000LL;
if (x % 5 < 2)
d.pop(); // remove
from the deque
else
d.push(x); // add
x into the deque
Res += d.getMin();
}
printf("%lld\n",Res);
return 0;
}
Algorithm realization – linked list
The
implementation of deque with pointers is advantageous because at each moment of
time we use exactly as much memory as we need to store all the data.
#include <stdio.h>
class deque
{
private:
struct node
{
int data;
node *next, *prev;
node()
{
prev = next = NULL;
}
node(int a)
{
data = a;
prev = next = NULL;
}
} *Head, *Tail;
public:
deque()
{
Head = Tail = NULL;
}
void push_back(int
a)
{
node *p = new node(a);
if(Head == NULL)
Head = Tail = p;
else
{
p->prev = Tail;
p->next = NULL;
Tail->next = p;
Tail = p;
}
}
void push_front(int
a)
{
node *p = new node(a);
if(Head == NULL)
Head = Tail = p;
else
{
p->next = Head;
p->prev = NULL;
Head->prev = p;
Head = p;
}
}
int pop_front(void)
{
node *p = Head;
int r = Head->data;
if(Head == Tail)
Head = Tail = NULL;
else
{
Head = Head->next;
Head->prev = NULL;
}
delete p;
return r;
}
int pop_back(void)
{
node *p = Tail;
int r = Tail->data;
if(Head == Tail)
Head = Tail = NULL;
else
{
Tail = Tail->prev;
Tail->next = NULL;
}
delete p;
return r;
}
int empty(void)
{
return Head == NULL;
}
int front(void)
{
return Head->data;
}
int back(void)
{
return Tail->data;
}
};
deque value, mn;
int x, i, n, a, b, c;
long long Res = 0;
int main(void)
{
scanf("%d %d %d %d %d",&n,&a,&b,&c,&x);
for(i = 1; i <= n; i ++)
{
x = ((1LL * a * x * x + 1LL * b * x + c) / 100) % 1000000LL;
if (x % 5 < 2) // remove from the deque
{
if (!value.empty())
{
if
(value.front() == mn.front()) mn.pop_front();
value.pop_front();
}
} else // add
value x into the deque
{
value.push_back(x);
while(!mn.empty() && (x <
mn.back())) mn.pop_back();
mn.push_back(x);
}
if (!mn.empty()) Res += mn.front();
}
printf("%lld\n",Res);
return 0;
}
Java realization
import java.util.*;
public class
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
LinkedList<Long> value = new
LinkedList<Long>();
LinkedList<Long> mn = new
LinkedList<Long>();
long n = con.nextLong(), a =
con.nextLong();
long b = con.nextLong(), c =
con.nextLong();
long x = con.nextLong(), Res
= 0;
for(long i = 1; i <= n; i ++)
{
x = ((a * x * x +
b * x + c) / 100) % 1000000;
if (x % 5 < 2)
{
if (value.isEmpty() == false)
{
if
(value.getFirst().equals(mn.getFirst())) mn.removeFirst();
value.removeFirst();
}
} else
{
value.addLast(x);
while(!mn.isEmpty() &&
(x < mn.getLast())) mn.removeLast();
mn.addLast(x);
}
if (!mn.isEmpty()) Res +=
mn.getFirst();
}
System.out.println(Res);
}
}