7125. Васин круг
Вася выписал n букв "X" и "E" по кругу. Вася подумал, что
получится 2n вариантов сделать это,
так как каждая буква может быть либо "X", либо "E". Однако
Петя заметил, что некоторые различные последовательности букв могут быть
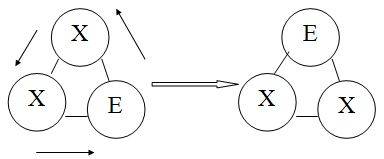
преобразованы друг в друга циклическим сдвигом (таким образом представляя одну
и ту же циклическую строку).
Например, строки
"XXE"-"XEX"-"EXX" на самом деле одинаковы.
Петя хочет знать, сколько
существует различных циклических строк из n
букв. Помогите ему это узнать.
Вход. Одно
число n (1 ≤ n ≤ 200000).
Выход. Вывести количество циклических
строк длины n.
Пример входа
3
Пример выхода
4
РЕШЕНИЕ
Теорема Пойа
Анализ алгоритма
Требуется найти количество
ожерелий из n бусинок, которые можно
получить в результате раскрашивания двумя красками (красками здесь являются
буквы "X" и "E").
Если ожерелье имеет n бусинок, каждая из которых может быть
покрашена в один из k цветов, то
количество различных ожерелий равно
![]()
Реализация алгоритма
Поскольку n ≤ 200000, то ответ будет большим числом. Воспользуемся
длинной арифметикой.
import
java.util.*;
import
java.math.*;
public class
Main
{
Вычисление функции Эйлера φ(n).
static long euler(long n)
{
long result
= n;
for(int i = 2; i <= Math.sqrt(n);i++)
{
if (n % i
== 0) result -= result / i;
while (n
% i == 0) n /= i;
}
if (n >
1) result -= result / n;
return
result;
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
BigInteger res = new
BigInteger("0");
Установим переменную k
равной количеству цветов.
BigInteger k = new
BigInteger("2");
int i, sq,
n = con.nextInt();
int up = sq
= (int)Math.sqrt(n);
if (sq * sq
== n) up--;
Перебираем делители i
числа n от 1 до ![]() . Если i – делитель
n, то n / i также будет
делителем n.
. Если i – делитель
n, то n / i также будет
делителем n.
for(i = 1;
i <= up; i++)
if (n % i
== 0)
{
res =
res.add(k.pow(n/i).multiply(BigInteger.valueOf(euler(i))));
res = res.add(k.pow(i).multiply(BigInteger.valueOf(euler(n/i))));
}
Отдельно обработаем случай, если n является полным квадратом.
if (sq * sq
== n)
res =
res.add(k.pow(i).multiply(BigInteger.valueOf(euler(i))));
res = res.divide(BigInteger.valueOf(n));
Выводим искомый ответ.
System.out.println(res);
}
}