7228. Сколько шестерок?

Сколько раз будет использована цифра 6, если записать подряд последовательные натуральные числа от a до b?

Вход. Два натуральных числа a и b (1 ≤ a, b ≤ 10⁹).

Выход. Количество цифр 6 в последовательных натуральных числах от a до b.

Пример входа	Пример выхода
1 89	19

РЕШЕНИЕ

рекурсия

Анализ алгоритма

Пусть f(n) равно количеству цифр 6 в последовательных натуральных числах от 1 до n. Тогда ответом будет значение f(b) – f(a – 1).

Пусть n оканчивается на цифру 9. Тогда в разряде единиц среди чисел от 1 до n шестерка встречается (n + 1) / 10 раз. А в остальных разрядах она встречается 10 * f(n / 10) раз. То есть

f(n) = (n + 1) / 10 + 10 * f(n / 10), если n оканчивается на 9

f(n) = 0 при n < 6

f(n) = 1 при 6 ≤ n < 10

Если n не оканчивается на цифру 9, то найдем такое наибольшее m < n, которое оканчивается на 9, после чего вычислим

. f(n) = f(m) + ,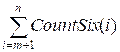

где CountSix(i) вычисляет количество шестерок в числе i.

Реализация алгоритма

Функция CountSix(n) подсчитывает количество шестерок в числе n.

int CountSix(int n)

{

int c = 0;

while(n > 0)

{

c += (n % 10 == 6);

n /= 10;

}

return c;

}

Вычисляем f(n) – количество шестерок в последовательных натуральных числах от 1 до n.

int f(int n)

{

if (n < 10)

return n >= 6;

int res = 0;

while(n % 10 != 9)

res += CountSix(n--);

return res + (n + 1) / 10 + f(n / 10) * 10;

}

Основная часть программы. Читаем входные данные. Если a > b, то меняем их местами.

scanf("%d %d",&a,&b);

if (a > b)

temp = a, a = b, b = temp;

Вычисляем и выводим f(b) – f(a – 1).

res = f(b) - f(a - 1);

printf("%d\n",res);